题目内容
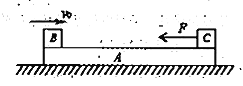
【题目】如图所示,一长为L的木板A放置在水平地面上,木板的两端分别放置着B.C两小块,三者质量分别为![]() .
. ![]() 和
和![]() ,A与地面、B与A、C与A间的动摩擦因数分别为
,A与地面、B与A、C与A间的动摩擦因数分别为![]() 、
、![]() 和
和![]() ,开始时三者均静止,现给物块B一水平向右的初速度
,开始时三者均静止,现给物块B一水平向右的初速度![]() ,同时给物块C一向左的水平拉力
,同时给物块C一向左的水平拉力![]() ,设最大静摩擦力等于滑动摩擦力,重力加速度为g,试求:
,设最大静摩擦力等于滑动摩擦力,重力加速度为g,试求:
(1)经过多长时间木板A开始运动;
(2)从A开始运动至B与C相遇的时间。
【答案】(1) ![]() ;(2)
;(2)![]()
【解析】(1)各接触面上的最大静摩擦力分别为:fAm=![]() μ×6mg=μmg,fBm=fCm=2μmg
μ×6mg=μmg,fBm=fCm=2μmg
B开始运动时,假定把A与C看成整体,整体水平方向所受合力为零,而:F=3μmg>fBm
故开始时C向左运动,A扔处于静止状态;设此时B、C的加速度大小分别为aB、aC.
由牛顿第二定律:
对B有:2μmg=2maB
对C有:3μmg-2μmg=maC
解得:aB=aC=μg
当B的速度减为零时,分析可以知道C对A的摩擦力大于地面对A的最大静摩擦力,此时A和B共同向左运动,因此A由静止开始运动需经过时间为:![]() .
.
(2)设A板开始运动前B、C的位移大小分别为xB、xC,由运动学公式得到:![]()
因B和C的运动反向对称,故xC=xB= ![]()
且B的速度减为零时,C的速度 vC=v0
A与B共同向左作匀加速运动的过程中,对A、B整体,由牛顿第二定律可得:
aAB=![]()
设再经过时间t,B与C相遇,此过程中B、C所运动的位移分别为xB′、xC′,由运动学公式可以得到:xC′-xB′=L-xB-xC
即:v0t+![]() aCt2-
aCt2-![]() aABt2=L-2×
aABt2=L-2×![]()
把![]() 代入上式可以得到:2(μg)2t2+5μgv0t-3v02=0
代入上式可以得到:2(μg)2t2+5μgv0t-3v02=0
解得:![]() .
.
点睛:本题的关键要求同学们能正确分析物体的受力情况和运动情况,分段运用牛顿第二定律和运动学公式进行研究,分析时要注意判断A的运动状态.