题目内容
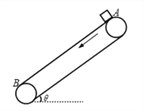
【题目】如下图所示，白色传送带A、B两端距离L=24m，以速度v0=8m/s逆时针匀速转动，并且传送带与水平面的夹角为θ=30°，现将一质量为m=2kg的煤块轻放在传送带的A端，煤块与传送带间动摩擦因数
，取g=10m/s2，则下列叙述正确的是（ ）
A. 煤块从A端运动到B端所经历时间为3.5s
B. 煤块从A端运动到B端重力的平均功率为120W
C. 煤块从A端运动到B端留下的黑色痕迹为4m
D. 煤块从A端运动到B端因摩擦产生的热量为24J
【答案】C
【解析】煤块放在传送带后受到沿斜面向下的滑动摩擦力作用，一定先向下做匀加速直线运动。设经过时间t1，煤块的速度与传送带相同，匀加速运动的加速度大小为a1，则根据牛顿第二定律得：mgsinθ+μmgcosθ=ma1，可得 a1=g（sinθ+μcosθ）=10×（sin30°+
×cos30°）=8m/s2；由 v0=a1t1 得 t1=1s；此过程通过的位移大小为 x1=
t1=
×1m=4m＜L。由于mgsinθ＞μmgcosθ．故煤块速度大小等于传送带速度大小后，继续匀加速向下运动，受到的滑动摩擦力沿斜面向上。设煤块接着做匀加速运动的加速度为a2，运动的时间为t2，则mgsinθ-μmgcosθ=ma2，可得 a2=g（sinθ-μcosθ）=10×（sin30°-0.5×cos30°）=2m/s2；由L-x1=v0t2+
a2t22，代入数据得：24-4=8t2+
×2×t22，解得 t2=2s。故煤块从A到B的运动时间是t=t1+t2=3s。故A错误。煤块从A端运动到B端时速度 v=v0+a2t2=8+2×2=12m/s，此时重力的瞬时功率为 P=mgvsinθ=2×10×12×sin30°=120W，故B错误。由于两个过程煤块与传送带间的相对位移大小（v0t1-x1）=[（L-x1）-v0t2]，所以煤块从A端运动到B端留下的黑色痕迹长度为 S=v0t1-x1=8×1-4=4m。故C正确。煤块从A端运动到B端因摩擦产生的热量为 Q=μmgcosθ{（v0t1-x1）+[（L-x1）-v0t2]}代入数据解得 Q=48J，故D错误。故选C。
