题目内容
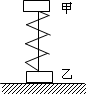
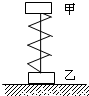
如图，甲、乙两木块用细绳连在一起，中间有一被压缩竖直放置的轻弹簧，乙放在水平地面上，甲、乙两木块质量分别为m1和m2，系统处于静止状态，此时绳的张力为F．在将细绳烧断的瞬间，甲的加速度为a，则此时乙对地面压力为m1（a+g）+m2g
m1（a+g）+m2g
．分析：根据甲的瞬间加速度，运用牛顿第二定律求出弹簧的弹力，从而再对乙分析，求出地面对乙的支持力．
解答：解：烧断细绳的瞬间，对甲有：F弹-m1g=m1a，则弹簧的弹力大小为F弹=m1g+m1a，此时对乙有：N=m2g+F弹=m1（a+g）+m2g．
故答案为：m1（a+g）+m2g
故答案为：m1（a+g）+m2g
点评：解决本题的关键能够选择研究对象，正确地进行受力分析，运用牛顿第二定律和共点力平衡进行求解
练习册系列答案
名校课堂系列答案
相关题目
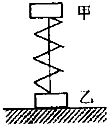如图，甲、乙两木块用细绳连在一起，中间有一被压缩竖直放置的轻弹簧，乙放在水平地面上，甲、乙两木块质量分别为m1和m2，系统处于静止状态，此时绳的张力为F．在将细绳烧断的瞬间，甲的加速度为a，则此时乙对地面压力为（ ）
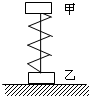如图，甲、乙两木块用细绳连在一起，中间有一被压缩竖直放置的轻弹簧，乙放在水平地面上，甲、乙两木块质量分别为m1和m2，系统处于静止状态，此时绳的张力为F．在将细绳烧断的瞬间，甲的加速度为a，则此时乙对地面压力为（ ）
