Question

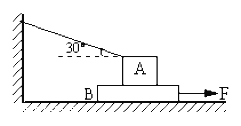
【题目】如图所示，水平地面上放置一个质量为m的物体，在与水平方向成θ角、斜向右上方的拉力F的作用下沿水平地面运动。设物体与地面间的动摩擦因数为μ，重力加速度为g.

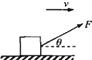
（1）若物体沿水平面向右匀速运动，求拉力F的大小；

（2）若物体在拉力F的作用下恰好不脱离地面，求拉力F和物体的加速度a的大小。

Answer 1

【答案】（1） （2）

【解析】试题分析：物体向右匀速运动，由平衡条件可得拉力F的大小；受力分析，关键抓住物体恰好不脱离地面，即N’=0，所以f’=0 ，根据牛顿第二定律即可求解。

（1）物体向右匀速运动，受力如图，由平衡条件可得：

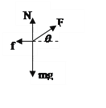
水平方向：Fsinθ+N-mg=0

竖直方向：Fcosθ-f=0

又因：f=N

联立可得：

（2）物体向右加速运动，受力如图，

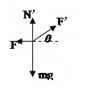
竖直方向：F’sinθ+N’-mg=0

物体恰好不脱离地面，即N’=0，

所以：f’=0

即F’sinθ-mg=0

联立解得：

水平方向由牛顿第二定律可得F’cosθ=ma

联立解得：