题目内容
(12分)空间中取坐标系Oxy，在第一象限内平行于y轴的虚线MN与y轴距离为d，从y轴到MN之间的区域充满一个沿y轴正方向的匀强电场，电场强度大小为E，如图所示。初速可忽略的电子经过一个电场直线加速后，从y轴上的A点以平行于x轴的方向射入第一象限区域，A点坐标为（0，h）。已知电子带电量大小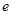
，质量
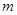，忽略电子重力的作用。则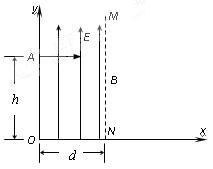
（1）若电子从B飞离MN，飞离时速度大小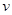
，且与初速度夹角
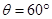，求AB间电势差
；
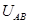（2）若加速电场的电势差可变，调节电势差，使电子经过x轴时的坐标为（2d，0），求加速电场的电势差U０ ．
(1) 
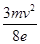(2) 
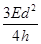
解析试题分析：解决本题的关键是理清电子的运动过程，先在加速电场中做加速运动，然后做类平抛运动，最后做匀速直线运动．在处理电子运动时将类平抛运动和匀速直线运动都分解为水平方向和竖直方向．
(1) 电子在垂直电场方向上做匀速直线运动，在沿电场方向上做匀加速直线运动，设电子在A为处速度为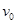
，则
飞离时有，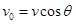
从A到B，由动能定理得：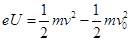
解得：
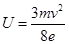有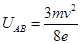
(2)设电子经过电场加速后速度为
，则由动能定理得：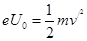
电子在偏转电场中做类平抛运动，根据牛顿第二定律及运动规律有：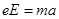
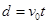
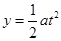
离开电场时，有
离开电场后匀速运动，有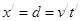
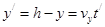
由以上各式解得加速电场的电势差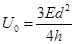
考点：本题考查带电粒子在匀强电场中的运动、动能定理的应用、电势差、运动的合成与分解、牛顿第二定律等知识，意在考查考生处理类平抛运动问题的能力．
练习册系列答案
相关题目
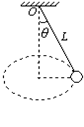
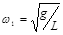做圆锥摆运动时，水平面受到的压力N是多大？
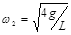做圆锥摆运动时，细绳的张力T为多大？
