题目内容
(16分)如图所示,ABCD为固定在竖直平面内的轨道,AB段光滑水平,BC段为光滑圆弧,对应的圆心角θ=37º,半径r=2.5m,CD段平直倾斜且粗糙,各段轨道均平滑连接,倾斜轨道所在区域有场强大小为E=2×l05N/C、方向垂直于斜轨向下的匀强电场.质量m=5×l0-2kg、电荷量q=+1×10-6C的小物体(视为质点)被弹簧枪发射后,沿水平轨道向左滑行,在C点以速度v0=3m/s冲上斜轨.以小物体通过C点时为计时起点,0.1s以后,场强大小不变,方向反向.已知斜轨与小物体间的动摩擦因数μ=0.25.设小物体的电荷量保持不变,取g=10m/s2,sin37º=0.60,cos37º=0.80. 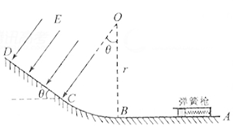
(1)求弹簧枪对小物体所做的功;
(2)电场方向改变前后,小物体的加速度各是多大;
(3)在斜轨上小物体能到达的最高点为P,求CP的长度.
(1)0.475J(2)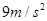
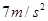 (3)0.57m
(3)0.57m
解析试题分析:(1)设弹簧枪对小物体做功为W,由动能定理得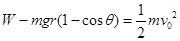 (3分)
(3分)
代人数据得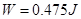 (2分)
(2分)
(2)设小物体通过C点进入电场后的加速度大小为a1,
由牛顿第二定律得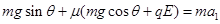 (2分) 得
(2分) 得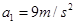 (1分)
(1分)
0.1s后,电场力反向,设小物体的加速度大小为a2,由牛顿第二定律得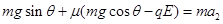 (2分) 得
(2分) 得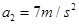 (1分)
(1分)
(3)小物体向上做匀减速运动,经t=0.1s后,速度达到v,有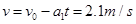 (1分)
(1分)
设运动的位移大小为s1,有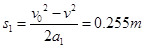 (1分)
(1分)
设小物体以此加速度运动到速度为0,位移大小为s2,有 (2分)
(2分)
设CP的长度为s,有 s=s1+s2=0.57m (1分)
考点:解答本题时先将小物体的运动分段,根据每一段运动受力情况判断运动性质的特点再选择动能定理、牛顿运动定律和运动学规律求解.

 =1.0×108 C/kg,粒子的重力和粒子间的相互作用都忽略不计,在粒子通过电场区域的极短时间内极板间的电压可以看作不变.求:
=1.0×108 C/kg,粒子的重力和粒子间的相互作用都忽略不计,在粒子通过电场区域的极短时间内极板间的电压可以看作不变.求:

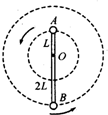
 ,那么物块能否紧贴圆环在竖直平面内做圆周运动。(写出详细分析、判定过程)(已知:
,那么物块能否紧贴圆环在竖直平面内做圆周运动。(写出详细分析、判定过程)(已知: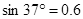 ;
;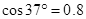 )
)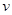 的
的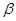 射线,B为金属网,A、B连接在电路上,电源电动势为
射线,B为金属网,A、B连接在电路上,电源电动势为 ,内阻为
,内阻为 ,滑动变阻器总阻值为
,滑动变阻器总阻值为 ,图中滑动变阻器滑片置于中点,A、B间距为d,M为荧光屏(足够大),它紧挨者金属网外侧,已知
,图中滑动变阻器滑片置于中点,A、B间距为d,M为荧光屏(足够大),它紧挨者金属网外侧,已知 ,不计
,不计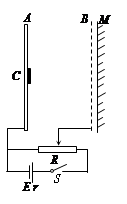

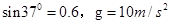 )求:
)求:
 ,质量
,质量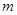 ,忽略电子重力的作用。则
,忽略电子重力的作用。则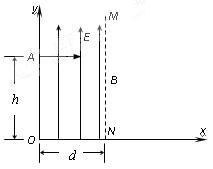
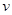 ,且与初速度夹角
,且与初速度夹角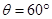 ,求AB间电势差
,求AB间电势差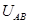 ;
;