题目内容
【题目】某同学用如图所示装置探究A、B两球在碰撞中动量是否守恒.该同学利用平抛运动测量两球碰撞前后的速度,实验装置和具体做法如下,图中PQ是斜槽,QR为水平槽.实验时先使A球从斜槽上某一固定位置G由静止开始滑下,落到位于水平地面的记录纸上,留下痕迹.重复上述操作10次,得到10个落点痕迹.再把B球放在水平槽上靠近槽末端的地方,让A球仍从位置G由静止开始滑下,和B球碰撞后,A、B球分别在记录纸上留下各自的落点痕迹.重复这种操作10次,并画出实验中A、B两小球落点的平均位置,图中F、E点是A碰B球前后的平均落点,J是B球的平均落点,O点是水平槽末端R在记录纸上的垂直投影点.其中米尺水平放置,且平行于G、R、O所在的竖直平面,米尺的零点与O点对齐.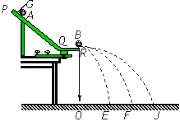
(1)现有下列器材,为完成本实验,哪些是必需的?请将这些器材前面的字母填在横线上 .
A.秒表
B.刻度尺
C.天平
D.圆规
(2)在以下选项中,哪些是本次实验必须进行的测量
A.水平槽上未放B球时,测量A球落点位置到O点的距离OF
B.A球与B球碰撞后,测量A球与B球落点位置到O点的距离OE、OJ
C.A球和B球在空间飞行的时间
D.测量G点相对于水平槽面的高度
(3)如果碰撞中动量守恒,根据图中各点间的距离,则下列式子正确的是 .
A.mA ![]() +mA
+mA ![]() =mB
=mB ![]()
B.mA ![]() =mA
=mA ![]() ﹣mB
﹣mB ![]()
C.mA ![]() =mA
=mA ![]() +mB
+mB ![]()
D.mA ![]() =mA
=mA ![]() +mB
+mB ![]() .
.
【答案】
(1)B,C,D
(2)A,B
(3)C
【解析】解:(1)碰撞后两球都做平抛运动,它们抛出点的高度相同,在空中的运动时间t相同,选择向右为正方向:
由动量守恒定律得:mAv0=mAv1+mBv2,
两边同时乘以时间t得:mAv0t=mAv1t+mBv2t,
则mAOE=mAOF+mBOJ,
实验需要验证的表达式为:mAOE=mAOF+mBOJ.
由公式可知,需要测量小球的质量,所以需要天平;需要测量小球的水平位移,所以需要使用刻度尺;小球的水平射程落点不是都落在同一个点上,需要取所有落点中靠近中间的点读数,即可取一个最小的圆的圆心,需要使用圆规;故需要选择的器材有:BCD
故选:BCD(2)A、水平槽上未放B球时,测量a球落点位置到O点的距离,即测量出碰撞前a球的速度,故A正确;
B、A球与B球碰撞后,测量A球落点位置到O点的距离,即测量出碰撞后A球的速度,故B正确;
C、小球在空中的运动时间t相同,不需要测量时间,故C错误;
D、不需要测量G点相对于水平槽面的高度,故D错误.
故选:AB(3)碰撞后两球都做平抛运动,它们抛出点的高度相同,在空中的运动时间t相同,选择向右为正方向:
由动量守恒定律得:mAv0=mAv1+mBv2,
两边同时乘以时间t得:mAv0t=mAv1t+mBv2t,
则mAOE=mAOF+mBOJ,
实验需要验证的表达式为:mAOE=mAOF+mBOJ.选项C正确.
故选:C
所以答案是:(1)BCD;(2)AB;(3)C



