题目内容
【题目】图中工人在推动一台割草机,施加的力大小为100N,方向与水平地面成30°角斜向下.割草机重300N,g取10m/s2 . 
(1)割草机作用在地面上的向下的压力为多大?
(2)若工人对割草机施加的作用力与图示方向相反,大小不变,则割草机作用在地面上的向下的压力又为多大?
(3)割草机割完草后,工人用最小的拉力拉它,使之做匀速运动,已知这个最小拉力为180N,则割草机与地面间的动摩擦因数及最小拉力与水平方向的夹角分别为多大?
【答案】
(1)解:如图1所示,分析割草机的受力情况,根据平衡条件得:
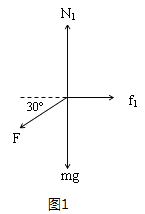
在竖直方向:N1=mg+Fsin30°
解得:N1=300+100×0.5=350(N),
由牛顿第三定律知对地面的压力大小为:N′=N=350N.
答:它对地面的压力F1大小是350N;
(2)若工人对割草机施加的作用力与图示反向,力的大小不变,则有:
N2=mg﹣Fsin30°=300N﹣100×0.5N=250N
则割草机作用在地面上向下的压力为250N.
答:割草机作用在地面上向下的压力又为250N.
(3)如图2所示,割草机沿水平方向做匀速直线运动,受到重力mg、拉力F、地面的支持力N和阻力f,如图,四个力的合力为零,则有:
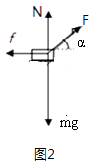
f=Fcosα
N+Fsinα=mg
又f=μN
联立得:F= ![]() =
= ![]() ,其中tanθ=
,其中tanθ= ![]()
所以当θ+α=90°,即tanα=μ时,F有最小值.
根据数学知识得到F的最小值为:Fmin= ![]()
由题F的最小值为:Fmin=180N
联立得: ![]() =180
=180
代入得: ![]() =180,
=180,
解得:μ=0.75,α=arctan0.75=37°
答:割草机和地面之间的动摩擦因数为0.75,最小拉力与水平方向夹角α为37°.
【解析】(1)以分析割草机为研究对象对割草机进行受力分析,列出竖直方向上的平衡方程,结合牛顿第三定律求出对地面的压力大小。
(2)工人对割草机施加的作用力与压力反向,力的大小不变,列式可直接求出。
(3),割草机沿水平方向做匀速直线运动,受到重力mg、拉力F、地面的支持力N和阻力f,四个力的合力为零,列式子导出力F与角度之间的关系,根据数学知识得到F的最小值。
【考点精析】利用滑动摩擦力对题目进行判断即可得到答案,需要熟知滑动摩擦力:利用公式f=μF N 进行计算,其中FN 是物体的正压力,不一定等于物体的重力,甚至可能和重力无关.或者根据物体的运动状态,利用平衡条件或牛顿定律来求解.