题目内容
(10分)如图18所示,光滑水平面AB与竖直面内的半圆形导轨在B点相切,半圆形导轨的半径为R.一个质量为m的物体将弹簧压缩至A点后由静止释放,在弹力作用下物体获得某一向右的速度后脱离弹簧,当它经过B点进入导轨的瞬间对轨道的压力为其重力的8倍,之后向上运动恰能到达最高点C.(不计空气阻力)试求:
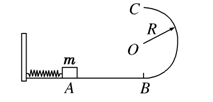
(1)物体在A点时弹簧的弹性势能;
(2)物体从B点运动至C点的过程中阻力所做的功;
(3)物体离开C点后落回水平面时的位置与B点的距离

(1)物体在A点时弹簧的弹性势能;
(2)物体从B点运动至C点的过程中阻力所做的功;
(3)物体离开C点后落回水平面时的位置与B点的距离
(1)3.5mgR (2)-mgR (3)2R
(1)设物体在B点的速度为vB,对轨道的压力为FNB,
则有:FNB-mg=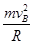 又FNB=8mg ∴
又FNB=8mg ∴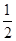 mvB2=3.5mgR
mvB2=3.5mgR
由能量转化与守恒定律可知:弹性势能Ep=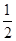 mvB2=3.5mgR……………….(4分)
mvB2=3.5mgR……………….(4分)
(2)设物体在C点的速度为vC
由题意可知:mg=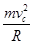
物体从B点运动到C点的过程中,设阻力做的功为W,由动能定理得W-2mgR=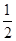 mvC2-
mvC2-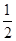 mvB2
mvB2
解得W=-mgR………………………(4分)
(3)物体离开C点后做平抛运动,设落地点与B点的距离为s,
由平抛运动规律得s=vCt,2R=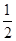 gt2
gt2
解得s=2R………………………. (2分)
本题考查圆周运动,在B点由弹力和重力提供向心力,由A点到B点,弹簧的弹性势能转化为物体的动能,由此可求得弹性势能,在C点由重力提供向心力,从B点到C点应用动能定理可求得克服阻力做功
则有:FNB-mg=
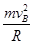 又FNB=8mg ∴
又FNB=8mg ∴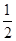 mvB2=3.5mgR
mvB2=3.5mgR由能量转化与守恒定律可知:弹性势能Ep=
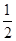 mvB2=3.5mgR……………….(4分)
mvB2=3.5mgR……………….(4分)(2)设物体在C点的速度为vC
由题意可知:mg=
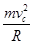
物体从B点运动到C点的过程中,设阻力做的功为W,由动能定理得W-2mgR=
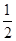 mvC2-
mvC2-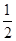 mvB2
mvB2解得W=-mgR………………………(4分)
(3)物体离开C点后做平抛运动,设落地点与B点的距离为s,
由平抛运动规律得s=vCt,2R=
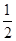 gt2
gt2解得s=2R………………………. (2分)
本题考查圆周运动,在B点由弹力和重力提供向心力,由A点到B点,弹簧的弹性势能转化为物体的动能,由此可求得弹性势能,在C点由重力提供向心力,从B点到C点应用动能定理可求得克服阻力做功

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
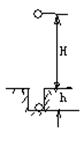
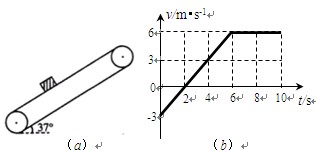
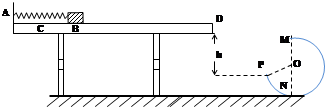

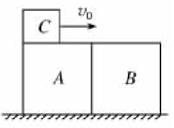
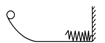
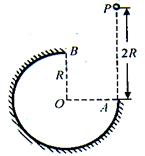
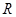 的圆弧轨道,半径
的圆弧轨道,半径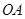 水平、
水平、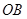 竖直,一个质量为
竖直,一个质量为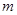 的小球自
的小球自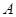 的正上方
的正上方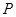 点由静止开始自由下落,小球沿轨道到达最高点
点由静止开始自由下落,小球沿轨道到达最高点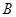 时恰好对轨道没有压力。已知
时恰好对轨道没有压力。已知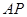 =2
=2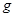 ,则小球从
,则小球从