题目内容
【题目】如图所示，光滑的薄平板，放置水平桌面上，平板右端与桌面相齐，在平板上距右端
处放一比荷为
的带电体B（大小可忽略），A长
，质量
。在桌面上方区域内有电场强度不同的匀强电场，
左侧电场强度为
，方向水平向右；右侧电场强度为左侧的5倍，方向水平向左。在薄平板A的右端施加恒定的水平作用力F，同时释放带电体B，经过一段时间后，在处带电体B与薄平板A分离，其后带电体B到达桌边缘时动能恰好为零，
求：
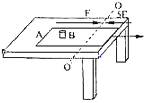
（1）处到桌面右边缘的距离；
（2）加在薄平板A上恒定水平作用力F的大小；
（3）从B与A分离开始计时，带电体B再一次回到分离点时运动的总时间。
【答案】（1）
；（2）
；（3）
【解析】
试题分析：（1）对B在
左侧运动时，
，设B到达
时的速度为
，则：
，对B在
右侧运动时，
，
，由几何关系知，
，
代入数据解得。
（2）对木板A，在B加速的时间内，
，
，
B在同一时间内加速的过程中，
，
对木板A，在B加速的时间内受力F的作用，由牛顿第二定律得，
，
代入数据解得。
（3）B在右侧电场中以v为初速度做匀减速直线运动，则
B在右侧电场中速度减小到零后再反向做匀加速直线运动，运动时间也为
B进入左侧电场中以v为初速度做匀减速直线运动，则
之后向右做匀加速直线运动，时间为
则总时间为：
。
练习册系列答案
综合自测系列答案
相关题目
