题目内容
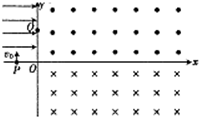 (2011?安徽三模)如图所示,在第二象限内有水平向右的匀强电场,在第一、第四象限内分别存在匀强磁场,磁感应强度大小相等,方向如图所示;现有一个带电粒子在该平面内从x轴上的P点,以垂直于x轴初速度v0进入匀强电场,恰好经过y轴上的Q点且与y轴成45°角射出电场,再经过一段时间又恰好垂直于x轴进入下面的磁场.已知OP之间的距离为d,(不计粒子的重力)求:
(2011?安徽三模)如图所示,在第二象限内有水平向右的匀强电场,在第一、第四象限内分别存在匀强磁场,磁感应强度大小相等,方向如图所示;现有一个带电粒子在该平面内从x轴上的P点,以垂直于x轴初速度v0进入匀强电场,恰好经过y轴上的Q点且与y轴成45°角射出电场,再经过一段时间又恰好垂直于x轴进入下面的磁场.已知OP之间的距离为d,(不计粒子的重力)求:(1)Q点的坐标;
(2)带电粒子自进入电场至在磁场中第二次经过x轴的时间.
分析:(1)带电粒子垂直进入匀强电场中做类平抛运动,竖直方向做匀速直线运动,水平方向做初速度为零的匀加速直线运动,运用平均速度分别表示水平位移和竖直位移.将粒子在Q点的速度进行分解,得到两个分速度的关系,即可求出带电粒子的坐标.
(2)画出带电粒子在磁场中运动的轨迹.由几何关系求出粒子圆周运动的半径,可求出圆周运动的周期,根据轨迹所对的圆心角求出粒子在磁场中运动的时间.粒子在电场中竖直方向做匀速直线运动,由Q的纵坐标和初速度可求出时间.即能求得总时间.
(2)画出带电粒子在磁场中运动的轨迹.由几何关系求出粒子圆周运动的半径,可求出圆周运动的周期,根据轨迹所对的圆心角求出粒子在磁场中运动的时间.粒子在电场中竖直方向做匀速直线运动,由Q的纵坐标和初速度可求出时间.即能求得总时间.
解答: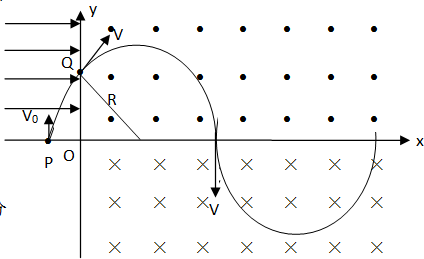 解:
解:
(1)设Q点的纵坐标为h,到达Q点的水平分速度为vx,则由类平抛运动的规律可知
h=v0t
d=
vxt
tan45°=
得h=2d,故Q点的坐标为(0,2d)
(2)粒子在磁场中的运动轨迹如图所示,设粒子在磁场中运动的半径为R,周期为T.则由几何关系可知:R=
?2d=2
d,
带电粒子进入磁场时的速度大小为 v=
v0
则粒子在磁场中运动的周期为 T=
=
d
设粒子在电场中的运动时间为t1
t1=
设粒子在磁场中的运动时间为t2
t2=
T+
T=
T=
d
则总时间为 t=t1+t2=
答:
(1)Q点的坐标为(0,2d);
(2)带电粒子自进入电场至在磁场中第二次经过x轴的时间为
.
 解:
解:(1)设Q点的纵坐标为h,到达Q点的水平分速度为vx,则由类平抛运动的规律可知
h=v0t
d=
| 1 |
| 2 |
tan45°=
| vx |
| v0 |
得h=2d,故Q点的坐标为(0,2d)
(2)粒子在磁场中的运动轨迹如图所示,设粒子在磁场中运动的半径为R,周期为T.则由几何关系可知:R=
| 2 |
| 2 |
带电粒子进入磁场时的速度大小为 v=
| 2 |
则粒子在磁场中运动的周期为 T=
| 2πR |
| v |
| 4π |
| v0 |
设粒子在电场中的运动时间为t1
t1=
| 2d |
| v0 |
设粒子在磁场中的运动时间为t2
t2=
| 3 |
| 8 |
| 1 |
| 2 |
| 7 |
| 8 |
| 7π |
| 2v0 |
则总时间为 t=t1+t2=
| (4+7π)d |
| 2v0 |
答:
(1)Q点的坐标为(0,2d);
(2)带电粒子自进入电场至在磁场中第二次经过x轴的时间为
| (4+7π)d |
| 2v0 |
点评:对于类平抛运动,采用运动的分解法研究,要抓住两个分运动的等时性.对于粒子在磁场中的圆周运动,画轨迹是关键.

练习册系列答案
相关题目

 (2011?安徽三模)如图所示,光滑斜面的倾角为30°轻绳通过两个滑轮与A相连,轻绳的另一端固定于天花板上,不计轻绳与滑轮的摩擦.物块A的质量为m不计滑轮的质量,挂上物块B后,当滑轮两边轻绳的夹角为90°时,A、B恰能保持静止,则物块B的质量为( )
(2011?安徽三模)如图所示,光滑斜面的倾角为30°轻绳通过两个滑轮与A相连,轻绳的另一端固定于天花板上,不计轻绳与滑轮的摩擦.物块A的质量为m不计滑轮的质量,挂上物块B后,当滑轮两边轻绳的夹角为90°时,A、B恰能保持静止,则物块B的质量为( ) (2011?安徽三模)在四川汶川的抗震救灾中,我国自主研制的“北斗一号”卫星导航系统,在抗震救灾中发挥了巨大作用.北斗导航系统又被称为“双星定位系统”,具有导航、定位等功能.“北斗”系统中两颗工作卫星均绕地心O在同一轨道上做匀速圆周运动,轨道半径为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置(如图所示).若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则以下判断中错误的是( )
(2011?安徽三模)在四川汶川的抗震救灾中,我国自主研制的“北斗一号”卫星导航系统,在抗震救灾中发挥了巨大作用.北斗导航系统又被称为“双星定位系统”,具有导航、定位等功能.“北斗”系统中两颗工作卫星均绕地心O在同一轨道上做匀速圆周运动,轨道半径为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置(如图所示).若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则以下判断中错误的是( ) (2011?安徽三模)水平面上有一边长为L的正方形,其a、b、c三个顶点上分别固定了三个等量的正点电荷Q,将一个电量为+q的点电荷分别放在正方形中心点O点和正方形的另一个顶点d点处,两处相比,下列说法正确的是( )
(2011?安徽三模)水平面上有一边长为L的正方形,其a、b、c三个顶点上分别固定了三个等量的正点电荷Q,将一个电量为+q的点电荷分别放在正方形中心点O点和正方形的另一个顶点d点处,两处相比,下列说法正确的是( )