题目内容
（1）质量m=1kg的重锤自由下落，在纸带上打出一系列的点如图4所示，O为第一个点，A、B、C为相邻的点，相邻计数点的时间间隔为0.02s，长度单位是cm，取g=9.8m/s2，求：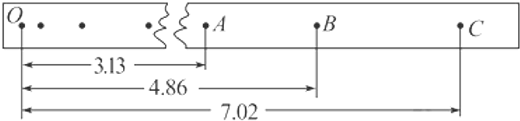
a．打点计时器打下计数点B时，物体的速度vB=
b．从点O到打下计数点B的过程中，物体重力势能的减少量△Ep=
△Ek=
（2）打出的另一条纸带如图，假设点AC间的距离为s1，点CE间的距离为s2，使用交流电的频率为f，根据这些条件计算重锤下落的加速度a=
．
a．打点计时器打下计数点B时，物体的速度vB=
0.97
0.97
m/s（保留两位有效数字）；b．从点O到打下计数点B的过程中，物体重力势能的减少量△Ep=
0.48
0.48
J，动能的增加量△Ek=
0.47
0.47
J（保留两位有效数字）．（2）打出的另一条纸带如图，假设点AC间的距离为s1，点CE间的距离为s2，使用交流电的频率为f，根据这些条件计算重锤下落的加速度a=
| (S2-S1)f2 |
| 4 |
| (S2-S1)f2 |
| 4 |
分析：纸带实验中，若纸带匀变速直线运动，测得纸带上的点间距，利用匀变速直线运动的推论，可计算出打出某点时纸带运动的瞬时速度和加速度，从而求出动能．根据功能关系得重力势能减小量等于重力做功的数值．
解答：解：（1）a、利用匀变速直线运动的推论
vB=
=
=0.97m/s
b、从点O到打下计数点B的过程中，物体重力势能的减少量△Ep=mgh=0.2×9.8×0.0486J=0.48J．
动能的增加量△Ek=EkB=
mvB2=0.47J
（2）根据运动学公式得：△x=at2，
a=
=
=
故答案为：（1）0.97，0.48，0.47．
（2）
vB=
| xAC |
| tAC |
| (0.0702-0.0313)m |
| 2×0.02s |
b、从点O到打下计数点B的过程中，物体重力势能的减少量△Ep=mgh=0.2×9.8×0.0486J=0.48J．
动能的增加量△Ek=EkB=
| 1 |
| 2 |
（2）根据运动学公式得：△x=at2，
a=
| △x |
| t2 |
| xCE-xAC | ||
(
|
| (S2-S1)f2 |
| 4 |
故答案为：（1）0.97，0.48，0.47．
（2）
| (S2-S1)f2 |
| 4 |
点评：要注意单位的换算和有效数字的保留．
求能量的变化量要注意研究的过程．
要知道打点频率和周期的关系．
求能量的变化量要注意研究的过程．
要知道打点频率和周期的关系．
练习册系列答案
阅读快车系列答案
相关题目
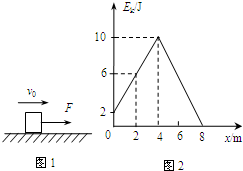
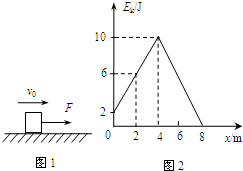如图1，质量m=1kg的物体，初速度为v0，方向水平向右．在向右的水平拉力F的作用下，沿粗糙水平面运动，位移为4m时，拉力 F停止作用，物体又运动了4m后停下来．其运动过程中的动能随位移的变化（Ek-x）图线如图2所示，重力加速度g取10m/s2，则（ ）
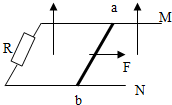如图所示，在水平面内有一对平行放置的金属导轨M、N，两导轨间距l=0.6m它们的电阻可忽略不计．阻值为2Ω的电阻R连接在MN的左端，垂直架在MN上的金属杆ab的电阻值r=1Ω，质量m=1kg，它与导轨间的接触电阻可以忽略，杆与导轨间的动摩擦因数μ=0.2，整个装置处在竖直向上的匀强磁场中，B=2T．金属杆ab在外力F作用下从静止开始做加速度a=1m/s2的匀加速直线运动．从运动开始计时，取g=10m/s2．求：
