题目内容
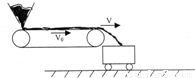
如图所示,用水平传送带向车厢装煤,传送带长L=4.5m,速度为v=3.5m/s.煤斗送到传送带左端的煤为每秒钟m=2.0kg,煤落到传送带上时速度忽略不计,动摩擦因数为μ=0.10,已知煤在传送带速度始终小于v,整个装置长时间连续工作.(g=10m/s2,结果保留2位有效数字)(1)传送带上总是有多少千克煤?
(2)某时刻开始计时,在一分钟时间内传送带对煤做多少功?
(3)传送带由电动机带动,不计转轴的摩擦,求电动机的输出功率.
【答案】分析:(1)煤落到传送带上时,相对传送带滑动,根据运动学公式,即可求出煤在带上滑动的时间,从而可求出共有多少煤在传送带上;
(2)根据一分钟时间,结合煤的速度,可求出传送带共输送多少煤,由煤获得动能,即可求出传送带对煤做的功;
(3)由电动机在每秒内输出的电能,即为煤获得的动能与摩擦阻力产生的内能之和,从而求出电动机的输出功率.
解答:解:(1)煤在传送带是做匀加速直线运动,
根据牛顿第二定律,则有a=μg=0.1×10m/s2=1m/s2
再由运动学公式,则有L=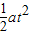
代入数据,解得:t=3s
因此传送带上总是有M=m×t=2×3kg=6kg
(2)传送带在每秒内煤获得的动能为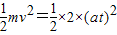 =
=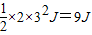
在一分钟时间内传送带对煤做的功,即为煤获得的动能,则有W=60×9J=540J
(3)根据能量守恒定律,则电动机每秒内输出的电能等于煤获得的动能与摩擦阻力产生的内能,
则有:E=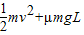 =
=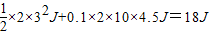
因此电动机的输出功率为18W.
答:(1)传送带上总是有6.0kg煤;
(2)某时刻开始计时,在一分钟时间内传送带对煤做5.4×102J功;
(3)传送带由电动机带动,不计转轴的摩擦,则电动机的输出功率18W.
点评:考查物体的运动情况与受力分析,掌握牛顿第二定律与运动学公式相综合解题,理解能量守恒定律的应用,注意求摩擦阻力做功时的位移是相对位移.
(2)根据一分钟时间,结合煤的速度,可求出传送带共输送多少煤,由煤获得动能,即可求出传送带对煤做的功;
(3)由电动机在每秒内输出的电能,即为煤获得的动能与摩擦阻力产生的内能之和,从而求出电动机的输出功率.
解答:解:(1)煤在传送带是做匀加速直线运动,
根据牛顿第二定律,则有a=μg=0.1×10m/s2=1m/s2
再由运动学公式,则有L=
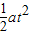
代入数据,解得:t=3s
因此传送带上总是有M=m×t=2×3kg=6kg
(2)传送带在每秒内煤获得的动能为
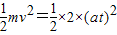 =
=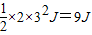
在一分钟时间内传送带对煤做的功,即为煤获得的动能,则有W=60×9J=540J
(3)根据能量守恒定律,则电动机每秒内输出的电能等于煤获得的动能与摩擦阻力产生的内能,
则有:E=
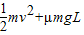 =
=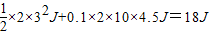
因此电动机的输出功率为18W.
答:(1)传送带上总是有6.0kg煤;
(2)某时刻开始计时,在一分钟时间内传送带对煤做5.4×102J功;
(3)传送带由电动机带动,不计转轴的摩擦,则电动机的输出功率18W.
点评:考查物体的运动情况与受力分析,掌握牛顿第二定律与运动学公式相综合解题,理解能量守恒定律的应用,注意求摩擦阻力做功时的位移是相对位移.

练习册系列答案
相关题目
 如图所示.一水平传送装置有轮半径为R=
如图所示.一水平传送装置有轮半径为R= (2012?聊城模拟)如图所示,一水平传送装置由轮半径均为R=
(2012?聊城模拟)如图所示,一水平传送装置由轮半径均为R=
 m的主动轮Q1和从动轮Q2及传送带等构成.两轮轴心相距lAB=8.0 m,轮与传送带不打滑.现用此装置运送一袋面粉,已知这袋面粉与传送带之间的动摩擦因数μ=0.4,这袋面粉中的面粉可不断地从袋中渗出.(g取10 m/s2)
m的主动轮Q1和从动轮Q2及传送带等构成.两轮轴心相距lAB=8.0 m,轮与传送带不打滑.现用此装置运送一袋面粉,已知这袋面粉与传送带之间的动摩擦因数μ=0.4,这袋面粉中的面粉可不断地从袋中渗出.(g取10 m/s2)
 的主动轮
的主动轮 和从动轮
和从动轮 及传送带等构成.两轮轴心相距
及传送带等构成.两轮轴心相距 ,轮与传送带不打滑.现用此装置运送一袋面粉(可视为质点),已知这袋面粉与传送带之间的动摩擦因数
,轮与传送带不打滑.现用此装置运送一袋面粉(可视为质点),已知这袋面粉与传送带之间的动摩擦因数 ,这袋面粉中的面粉可不断地从袋中少量渗出.(
,这袋面粉中的面粉可不断地从袋中少量渗出.( )
) 
 的速度匀速运动时,将这袋面粉由左端
的速度匀速运动时,将这袋面粉由左端 点轻放在传送带上后,这袋面粉由
点轻放在传送带上后,这袋面粉由 ,渗出面粉的质量不计,求摩擦力对这袋面粉所做的功?
,渗出面粉的质量不计,求摩擦力对这袋面粉所做的功? 点,传送带的速度至少多大?
点,传送带的速度至少多大?