题目内容
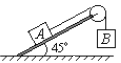
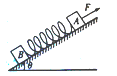
【题目】如图所示,A、B两木块的重力均为50 N,放在倾角θ=37°的斜面上,A、B与斜面间的动摩擦因数均为0.5。在沿斜面向上的大小为60 N的力F作用下,A、B静止在斜面上,此时,与A、B相连的轻弹簧被拉伸了3 cm,弹簧的劲度系数为400 N /m。则下列说法正确的是( )
A. A、B所受的摩擦力均为零
B. B受的摩擦力为2N,方向沿斜面向上
C. A受的摩擦力为18N,方向沿斜面向下
D. B受的摩擦力为18N,方向沿斜面向上
【答案】CD
【解析】试题分析:根据胡克定律可知,弹簧的弹力 F弹=k△x=400×0.03N=12N
B处于静止状态,受力平衡,设B受到的摩擦力方向向下,根据平衡条件得:F弹-Gsin37°-fB=0
解得:fB=-18N,则B受的静摩擦力为18N,方向沿斜面向上
A处于静止状态,受力平衡,设A受到的静摩擦力方向沿斜面向下,根据平衡条件得:
F-F弹-Gsin37°-fA=0
解得:fA=18N,方向沿斜面向下.故CD正确,AB错误。
故选:CD。

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目