题目内容
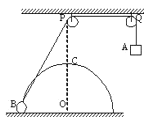
【题目】如图所示，在距水平地面高均为0.4m处的P、Q两处分别固定两光滑小定滑轮，细绳跨过滑轮，一端系一质量为mA=2.75kg的小物块A，另一端系一质量为mB=1kg的小球B；半径R=0.3m的光滑半圆形轨道竖直地固定在地面上，其圆心O在P点的正下方，且与两滑轮在同一竖直平面内，小球B套在轨道上，静止起释放该系统，则小球B被拉到离地_____________m高时滑块A与小球B的速度大小相等，小球B从地面运动到半圆形轨道最高点时的速度大小为_____________m/s．
【答案】0.225； 4
【解析】
当绳与轨道相切时滑块与小球速度相等，由几何知识求得此时小球B的高度．小球B到半圆形轨道最高点时，A物的速度为零，对系统，运用动能定理列式，即可求出B球到最高点时的速度大小．
当绳与轨道相切时滑块与小球速度相等，（B速度只沿绳），由几何知识得R2=h
，所以有：
．
小球B从地面运动到半圆形轨道最高点时，A物的速度为零，即vA=0，
对系统，由动能定理得：mAg[
-（PO-R）]=mBgR+
mvB2
代入数据解得：vB=4m/s
练习册系列答案
阅读快车系列答案
相关题目
