题目内容
如图1在真空中,O点放置一点电荷D,MN与PS间为无电场区域,A、B为两平行金属板,两板间距离为b,板长为2b,O1O2为两板的中心线.现有一质量为m、电荷量为q的带正电粒子从距O点正下方R处,以速度Vo垂直MN向左进入点电荷D的电场,绕O点做匀速圆周运动,通过无电场区域后,恰好沿O1O2方向进入板间,此时给A、B板加上如图2所示的电压u,最后粒子刚好以平行于B板的速度,从B板的边缘飞出,不计平行金属板两端的边缘效应及粒子所受重力,已知静电力常量为K.
(1)求点电荷D的电量Q,并判断其电性
(2)求交变电压的周期T和电压Uo.
【答案】分析:本题(1)的关键是根据牛顿第二定律求出点电荷的电量.
(2)题的难点是找出粒子离开电场的时间t与交变电压周期T的关系式以及刚好离开电场时的偏转位移与交变周期倍数的关系,然后结合类平抛规律即可求解.
解答:解:(1)对粒子在做圆周运动时,库仑力提供向心力,则有:
 =
= ,解得Q=
,解得Q=
由于粒子带正电,故点电荷带负电.
(2)对粒子在板间运动时,设运动时间为t,
则:2b=vt
 =2n
=2n
又知t=nT(n=1,2,3…)
解得T=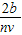 ,
,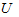 =
= (n=1,2,3…)
(n=1,2,3…)
答:(1)点电荷D的电量Q= ,点电荷带负电.
,点电荷带负电.
(2)交变电压的周期T= ,电压
,电压 =
= (n=1,2,3,…)
(n=1,2,3,…)
点评:解决动力学问题的关键是明确物理过程,根据不同的物理过程列式求解即可.
(2)题的难点是找出粒子离开电场的时间t与交变电压周期T的关系式以及刚好离开电场时的偏转位移与交变周期倍数的关系,然后结合类平抛规律即可求解.
解答:解:(1)对粒子在做圆周运动时,库仑力提供向心力,则有:
 =
= ,解得Q=
,解得Q=
由于粒子带正电,故点电荷带负电.
(2)对粒子在板间运动时,设运动时间为t,
则:2b=vt
 =2n
=2n
又知t=nT(n=1,2,3…)
解得T=
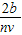 ,
,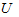 =
= (n=1,2,3…)
(n=1,2,3…) 答:(1)点电荷D的电量Q=
 ,点电荷带负电.
,点电荷带负电.(2)交变电压的周期T=
 ,电压
,电压 =
= (n=1,2,3,…)
(n=1,2,3,…)点评:解决动力学问题的关键是明确物理过程,根据不同的物理过程列式求解即可.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 如图,在真空中的O点放一点电荷Q=4.0×10-9C,直线MN过O点,OM=20cm,M点放有一点电荷q=-2×10-10C,如图所示,(静电力常量k=9.0×109N?m2/C2)求:
如图,在真空中的O点放一点电荷Q=4.0×10-9C,直线MN过O点,OM=20cm,M点放有一点电荷q=-2×10-10C,如图所示,(静电力常量k=9.0×109N?m2/C2)求:
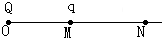 在真空中的O点放置一个Q=+1.0×10-9C的点电荷,直线MN通过O点,OM的距离r=10cm,在M点放置另一个q=-1.0×10-12C的点电荷,如图所示.求:
在真空中的O点放置一个Q=+1.0×10-9C的点电荷,直线MN通过O点,OM的距离r=10cm,在M点放置另一个q=-1.0×10-12C的点电荷,如图所示.求:
