题目内容
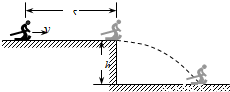
 (1)在冬天,高为h=1.25m的平台上,覆盖一层薄冰,一乘雪橇的滑雪爱好者,从距平台边缘s=24m处以一定的初速度向平台边缘滑去,如图所示,当他滑离平台即将着地时的瞬间,其速度方向与水平地面的夹角为θ=45°,取重力加速度g=10m/s2.求:
(1)在冬天,高为h=1.25m的平台上,覆盖一层薄冰,一乘雪橇的滑雪爱好者,从距平台边缘s=24m处以一定的初速度向平台边缘滑去,如图所示,当他滑离平台即将着地时的瞬间,其速度方向与水平地面的夹角为θ=45°,取重力加速度g=10m/s2.求:1 滑雪者着地点到平台边 缘的水平距离是多大;
2 若平台上的薄冰面与雪橇间的动摩擦因素为μ=0.05,则滑雪者的初速度是多大?
(2)在某星球表面用弹簧秤称得质量为m的砝码重力为F,忽略该星球的自转,宇宙飞船在靠近该星球表面空间飞行时,测得其环绕周期为T.根据上述数据,试求该星球的质量.
分析:(1)根据平抛运动的高度求出运动的时间,从而得出竖直方向上的分速度,通过速度的方向,求出平抛运动的初速度,结合时间求出水平距离.
对滑雪者在平台上的运动运用动能定理,求出滑雪者的初速度.
(2)根据万有引力提供向心力,结合运行的周期,求出星球的质量.
对滑雪者在平台上的运动运用动能定理,求出滑雪者的初速度.
(2)根据万有引力提供向心力,结合运行的周期,求出星球的质量.
解答:解:(1)把滑雪爱好者着地时的速度vt分解为如右图所示的v0、v┴两个分量
由 h=
gt2 得t=0.5s
则 v┴=gt=5 m/s v0=v┴tan45°=5 m/s
着地点到平台边缘的水平距离:x=v0t=2.5m
(2)滑雪者在平台上滑动时,受到滑动摩擦力作用而减速度,由动能定理
-μmgs=
mv02-
mv2
得:v=7m/s,即滑雪者的初速度为7m/s.
(2)设星球的质量为M,半径为R,由万有引力定律有:G
=F…①
设飞船的质量为 m′,其绕星球作圆周运动时有:
=m′R(
)2…②
联合①②式得M=
.
答:(1)滑雪者着地点到平台边 缘的水平距离是5m,滑雪者的初速度是7m/s.
(2)该星球的质量M=
.
由 h=
| 1 |
| 2 |
则 v┴=gt=5 m/s v0=v┴tan45°=5 m/s
着地点到平台边缘的水平距离:x=v0t=2.5m
(2)滑雪者在平台上滑动时,受到滑动摩擦力作用而减速度,由动能定理
-μmgs=
| 1 |
| 2 |
| 1 |
| 2 |
得:v=7m/s,即滑雪者的初速度为7m/s.
(2)设星球的质量为M,半径为R,由万有引力定律有:G
| Mm |
| R2 |
设飞船的质量为 m′,其绕星球作圆周运动时有:
| GMm′ |
| R2 |
| 2π |
| T |
联合①②式得M=
| F3T4 |
| 16Gm3π4 |
答:(1)滑雪者着地点到平台边 缘的水平距离是5m,滑雪者的初速度是7m/s.
(2)该星球的质量M=
| F3T4 |
| 16Gm3π4 |
点评:本题考查了平抛运动的规律、动能定理以及万有引力理论的综合运用,难度适中,需加强这方面题型的训练.

练习册系列答案
相关题目

 在冬天,高为h=1.25m的平台上,覆盖了一层冰,一乘雪橇的滑雪爱好者,从距平台边缘s=24m处以一定的初速度向平台边缘滑去,如图所示,当他滑离平台即将着地时的瞬间,其速度方向与水平地面的夹角为θ=45°,取重力加速度g=10m/s2.求:
在冬天,高为h=1.25m的平台上,覆盖了一层冰,一乘雪橇的滑雪爱好者,从距平台边缘s=24m处以一定的初速度向平台边缘滑去,如图所示,当他滑离平台即将着地时的瞬间,其速度方向与水平地面的夹角为θ=45°,取重力加速度g=10m/s2.求: 在冬天,高为h=1.25m的平台上,覆盖了一层冰,一乘雪橇的滑雪爱好者,从距平台边缘s=24m处以5m/s的初速度向平台边缘匀速滑去,如图所示,不计空气阻力,取重力加速度g=10m/s2.求:
在冬天,高为h=1.25m的平台上,覆盖了一层冰,一乘雪橇的滑雪爱好者,从距平台边缘s=24m处以5m/s的初速度向平台边缘匀速滑去,如图所示,不计空气阻力,取重力加速度g=10m/s2.求: