题目内容
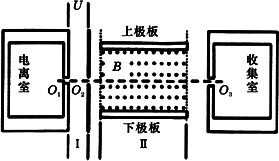
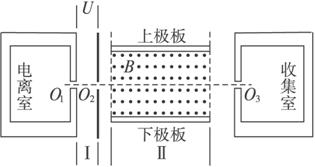
24.有人设想用如图所示的装置来选择密度相同、大小不同的球状纳米粒子。粒子在电离室中电离后带正电，电量与其表面积成正比。电离后，粒子缓慢通过小孔O1进入极板间电压为U的水平加速电场区域I，再通过小孔O2射入相互正交的恒定匀强电场、磁场区域Ⅱ，其中磁场的磁感应强度大小为B，方向如图。收集室的小孔O3与O1、O2在同一条水平线上。半径为r0的粒子，其质量为m0、电量为q0，刚好能沿O1O3直线射入收集室。不计纳米粒子重力。(V球=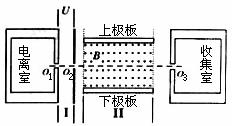
，S球=
) 
（1）试求图中区域Ⅱ的电场强度；
（2）试求半径为r的粒子通过O2时的速率；
（3）讨论半径r≠ro的粒子刚进入区域Ⅱ时向哪个极板偏转。
（1）
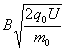，电场强度方向竖直向上
（2）
（3），粒子会向上极板偏转；
，粒子会向下极板偏转。
解析:（1）设半径为r0的粒子加速后的速度为v0，则
v总=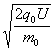
设区域Ⅱ内电场强度为E，则
v0q0B=q0E
E=v0B=B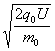
电场强度方程竖直向上。
（2）设半径为r的粒子的质量为m、带电量为q、被加速后的速度为v，则
m=（
）
q=（
）2q0
由 
mv2=qU 得
v=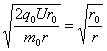
v0
（3）半径为r的粒子，在刚进入区域Ⅱ时受到合力为
F合=qE-qvB=qB（v0-v）
由v=
v0可知，当
r＞r0时，v＜v0，F合＞0，粒子会向上极板偏转；
r＜r0时，v＞v0，F合＜0，粒子会向下极板偏转。
练习册系列答案
相关题目
（2012?许昌模拟）当前，高楼遇险逃生措施及训练引起高度关注．有人设想在消防云梯上再伸出轻便的滑竿解救受困人员，解决云梯高度不够高的问题．如图所示，在一次消防演习中模拟解救被困人员，为了安全，被困人员使用安全带上挂钩挂在滑竿上从高楼A点沿滑杆下滑逃生．滑杆由AO、OB两段直杆通过光滑转轴在O处连接，将被困人员和挂钩理想化为质点，且通过O点的瞬间没有机械能的损失．AO长为L1=5m，OB长为L2=10m．竖直墙与云梯上端点B的间距d=11m．滑杆A端用挂钩钩在高楼的固定物上，可自由转动．B端用铰链固定在云梯上端．挂钩与两段滑杆间动摩擦因数均为μ=0.8．（g=10m/s2）
πr3，S球＝4πr2)
)
πr3,S球=4πr2)