题目内容
人骑自行车由静到动,除了要增加人和车的动能以外,还要克服空气及其他阻力做功.为了测量人骑自行车的功率,如图1第一活动小组进行了如下实验:在离出发线5m、10m、20m、30m、…70m的地方分别划上8条计时线,每条计时线上附近站几个学生,手持秒表测运动时间.听到发令员的信号后,受测者全力骑车由出发线启动,同时全体学生都开始计时.自行车每到达一条计时线,站在该计时线上的几个学生就停止计时,记下自行车从出发线到该条计时线的时间.
实验数据记录如下(每个计时点的时间都取这几个同学计时的平均值),并计算出各段的平均速度:
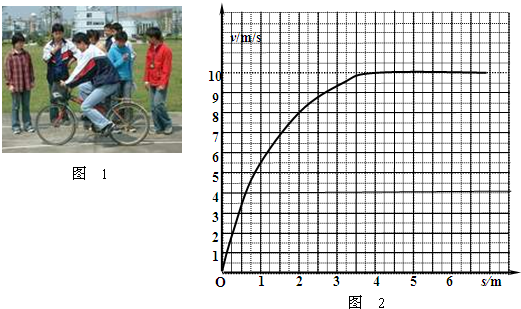
第二小组通过测出自行车在各点的速度,作出了V-S图(图2).第9秒时运动了40m的数据本次实验中,学生和自行车总质量约为75kg,设运动过程中,学生和自行车所受阻力与其速度大小成正比,整个过程中该同学骑车的功率P保持不变.
(1)第一小组的同学通过分析认为:因为自行车在每一路段内的速度变化不是很大,因此可以用每一段的平均速度代替该段的
速度.则在20m-30m路段的平均阻力f1与30m-40m路段的平均阻力f2之比f1:f2为多少?该同学的骑车的功率约为多少?速度为
6m/s时的加速度多大?
(2)第二组的同学结合图和(其曲线与横坐标在S=40m内所围的面积总为56格),测出的该同学的骑车的功率约为多少?
实验数据记录如下(每个计时点的时间都取这几个同学计时的平均值),并计算出各段的平均速度:
| 运动距 离s(m) | 0 | 5 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | |||||||
| 运动时间t(s) | 0 | 2.4 | 4.2 | 6.3 | 7.8 | 9.0 | 10.0 | 11.0 | 12.0 | |||||||
| 各段速度(m/s) | 2.08 | 2.78 | 4.76 | 6.67 | 8.33 | 10.0 | 10.0 | 10.0 | ||||||||
(1)第一小组的同学通过分析认为:因为自行车在每一路段内的速度变化不是很大,因此可以用每一段的平均速度代替该段的
速度.则在20m-30m路段的平均阻力f1与30m-40m路段的平均阻力f2之比f1:f2为多少?该同学的骑车的功率约为多少?速度为
6m/s时的加速度多大?
(2)第二组的同学结合图和(其曲线与横坐标在S=40m内所围的面积总为56格),测出的该同学的骑车的功率约为多少?

分析:(1)结合f=kv,通过速度之比求出阻力大小之比.在9s后做匀速直线运动,牵引力等于阻力,对开始运动到9s内运用动能定理,求出比例系数,从而根据匀速运动时牵引力等于阻力求出骑车的功率.结合功率与速度的关系求出牵引力的大小,根据牛顿第二定律求出加速度的大小.
(2)根据动能定理,结合在9s内滑行的位移,功率与最大速度的关系,求出比例系数和功率的大小.
(2)根据动能定理,结合在9s内滑行的位移,功率与最大速度的关系,求出比例系数和功率的大小.
解答:解:(1)设f=KV
f1:f2=V1:V2=6.67:8.33=0.8
9秒时,f=KV=10K,P=fV=100K
在开始运动9秒内,根据动能定理可知:
mv2=Pt-f1s1-f2s2-f3s3-f4s4-f5s5
代入数据解得:k=5.53(Ns/m)
P=553W
V=6m/s时
-kv=ma
-5.53×6=75a
解得a=0.79m/s2.
(2)在开始运动9秒内,根据动能定理可知
mv2=Pt-fs
代入数据解得 K=6Ns/m P=600W
答:(1)20m-30m路段的平均阻力f1与30m-40m路段的平均阻力f2之比f1:f2为0.8.该同学的骑车的功率553W.速度为6m/s时的加速度为0.79m/s2.
(2)该同学的骑车的功率为600W.
f1:f2=V1:V2=6.67:8.33=0.8
9秒时,f=KV=10K,P=fV=100K
在开始运动9秒内,根据动能定理可知:
| 1 |
| 2 |
代入数据解得:k=5.53(Ns/m)
P=553W
V=6m/s时
| P |
| v |
| 553 |
| 6 |
解得a=0.79m/s2.
(2)在开始运动9秒内,根据动能定理可知
| 1 |
| 2 |
代入数据解得 K=6Ns/m P=600W
答:(1)20m-30m路段的平均阻力f1与30m-40m路段的平均阻力f2之比f1:f2为0.8.该同学的骑车的功率553W.速度为6m/s时的加速度为0.79m/s2.
(2)该同学的骑车的功率为600W.
点评:解决本题的关键知道功率与速度的关系,结合动能定理进行求解.

练习册系列答案
相关题目
(2011年福建六校联考)人骑自行车由静到动,除了要增加人和车的动能以外,还要克服空气及其他阻力做功.为了测量人骑自行车的功率,第一小组进行了如下实验:在离出发线5 m、10 m、20 m、30 m、…70 m的地方分别划上8条计时线,每条计时线附近站几个学生,手持秒表测运动时间.听到发令员的信号后,受测者全力骑车由出发线启动,同时全体学生都开始计时.自行车每到达一条计时线,站在该计时线上的几个学生就停止计时,记下自行车从出发线到该条计时线的时间.实验数据记录如下(每个计时点的时间都取这几个同学计时的平均值),并计算出各段的平均速度:
| 运动距离s(m) | 0 | 5 | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
| 运动时间t(s) | 0 | 2.4 | 4.2 | 6.3 | 7.8 | 9.0 | 10.0 | 11.0 | 12.0 |
| 各段速度(m/s) | | 2.08 | 2.78 | 4.76 | 6.67 | 8.33 | 10.0 | 10.0 | 10.0 |
第二小组通过测出自行车在各点的速度,作出了v—s图4-2-9.本次实验中,学生和自行车总质量约为75 kg,设运动过程中,学生和自行车所受阻力与其速度大小成正比,整个过程中该学生骑车的功率P保持不变.

图4-2-9
(1)第一小组的学生通过分析认为:因为自行车在每一路段内的速度变化不是很大,因此可以用每一段的平均速度代替该段的速度,则在20 m~30 m路段的平均阻力f1与30 m~40 m路段的平均阻力f2之比f1∶f2为多少?被测学生骑车的功率约为多少?速度为6 m/s时的加速度为多大?
(2)第二小组的学生结合图和曲线(曲线与横坐标在s=40 m内所围的区域共56格),测出的被测学生骑车的功率约为多少?

 人骑自行车由静到动,除了要增加人和车的动能以外,还要克服空气及其他阻力做功.为了测量人骑自行车的功率,某活动小组进行了如下实验:在离出发线5m、10m、20m、30m、…70m的地方分别划上8条计时线,每条计时线附近站几个学生,手持秒表.听到发令员的信号后,受测者全力骑车由出发线启动,同时全体学生都开始计时.自行车每到达一条计时线,站在该计时线上的几个学生就停止计时,记下自行车从出发线到该条计时线的时间.实验数据记录如下(每个计时点的时间都取这几个同学计时的平均值):
人骑自行车由静到动,除了要增加人和车的动能以外,还要克服空气及其他阻力做功.为了测量人骑自行车的功率,某活动小组进行了如下实验:在离出发线5m、10m、20m、30m、…70m的地方分别划上8条计时线,每条计时线附近站几个学生,手持秒表.听到发令员的信号后,受测者全力骑车由出发线启动,同时全体学生都开始计时.自行车每到达一条计时线,站在该计时线上的几个学生就停止计时,记下自行车从出发线到该条计时线的时间.实验数据记录如下(每个计时点的时间都取这几个同学计时的平均值):