题目内容
【题目】一轻质弹簧，两端连接两滑块A和B，已知mA=0.99kg，mB=3kg，放在光滑水平桌面上，开始时弹簧处于原长．现滑块A被水平飞来的质量为mC=10g，速度为400m/s的子弹击中，且没有穿出，如图所示，试求：
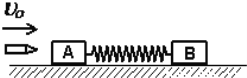
(1)子弹击中A的瞬间A和B的速度分别为多少？
(2)以后运动过程中弹簧的最大弹性势能？
(3)弹簧恢复原长时，两滑块的速度分别为多少？
【答案】(1)vA=4m/s,vB=0 (2)6J (3)
；
【解析】
子弹击中A的瞬间，子弹和A组成的系统水平方向动量守恒，据此可列方程求解A的速度，此过程时间极短，B没有参与，速度仍为零．以子弹、滑块A、B和弹簧组成的系统为研究对象，当三者速度相等时，系统损失动能最大则弹性势能最，根据动量守恒和功能关系可正确解答．
(1)子弹击中滑块A的过程，子弹与滑块A组成的系统动量守恒有：mCv0=（mC+mA）vA
解得：vA=4m/s
子弹与A作用过程时间极短，B没有参与，速度仍为零，故：vb=0．
故子弹击中A的瞬间A和B的速度分别为：vA=4m/s，vb=0．
(2)对子弹、滑块A、B和弹簧组成的系统，A、B速度相等时弹性势能最大．
根据动量守恒定律和功能关系可得：mCv0=（mC+mA+mB）v
由此解得：v=1m/s
根据功能关系可得：
故弹簧的最大弹性势能为6J．
(3)设B动能最大时的速度为
，A的速度为
，
由系统的动量守恒可得：
当弹簧恢复原长时，B的动能最大，
根据功能关系有：
解得：
；
练习册系列答案
小学期末标准试卷系列答案
相关题目
