题目内容
1. 汤姆孙提出的测定带电粒子的比荷($\frac{q}{m}$)的实验原理如图所示.带电粒子经过电压为U的加速电场加速后,垂直于磁场方向进入宽为L的有界匀强磁场,带电粒子穿过磁场时发生的偏转位移是d,若磁场的磁感应强度为B.则带电粒子的比荷为( )
汤姆孙提出的测定带电粒子的比荷($\frac{q}{m}$)的实验原理如图所示.带电粒子经过电压为U的加速电场加速后,垂直于磁场方向进入宽为L的有界匀强磁场,带电粒子穿过磁场时发生的偏转位移是d,若磁场的磁感应强度为B.则带电粒子的比荷为( )| A. | $\frac{q}{m}$=$\frac{2U{d}^{2}}{{B}^{2}({d}^{2}+{L}^{2})^{2}}$ | B. | $\frac{q}{m}$=$\frac{4U{d}^{2}}{{B}^{2}({d}^{2}+{L}^{2})^{2}}$ | ||
| C. | $\frac{q}{m}$=$\frac{6U{d}^{2}}{{B}^{2}({d}^{2}+{L}^{2})^{2}}$ | D. | $\frac{q}{m}$=$\frac{8U{d}^{2}}{{B}^{2}({d}^{2}+{L}^{2})^{2}}$ |
分析 粒子在电场中做加速运动,由动能定理可求得粒子进入磁场时的速度;
粒子在磁场中做匀速圆周运动,由洛仑兹力充当向心力可求得粒子的比荷.
解答 解:由动能定理可知,Uq=$\frac{1}{2}$mv2;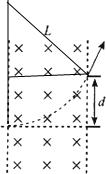
设带电粒子在磁场中运动的半径为r,则由几何关系可知:
r2=L2+(r-d)2;
解得r=$\frac{{L}^{2}+{d}^{2}}{2d}$
由牛顿第二定律可知:
Bqv=m$\frac{{v}^{2}}{r}$
联立解得:$\frac{q}{m}$=$\frac{8U{d}^{2}}{B({d}^{2}+{L}^{2})^{2}}$,故D正确,ABC错误.
故选:D.
点评 本题考查带电粒子在带电粒子在磁场中运动问题的应用;要注意洛仑兹力在磁场中运动解题关键为“定圆心,找半径”由牛顿第二定律求解,而在电场中要注意应用动能定理的应用.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
10.用比值法定义的物理量是物理学中常用的一种方法,以下物理量是用该公式比值法定义的是( )
| A. | 电流强度 I=$\frac{U}{R}$ | B. | 电场强度 E=$\frac{F}{q}$ | ||
| C. | 电容器的电容 C=$\frac{Q}{U}$ | D. | 电阻R=ρ$\frac{L}{S}$ |
11.下列有关电流的说法中正确的是( )
| A. | 导体中电荷的热运动形成了电流 | |
| B. | 导体中的电荷的定向移动形成了电流 | |
| C. | 电流的方向就是电子运动的方向 | |
| D. | 电流强度是矢量 |
8.在匀速圆周运动时,不变的物理量是( )
| A. | 周期 | B. | 线速度 | C. | 角速度 | D. | 向心力 |
15.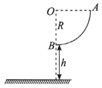 如图所示,AB为四分之一固定轨道,半径R=0.5m.一质量m=1kg的小滑块从圆弧轨道A端由静止释放,小滑块在圆弧轨道B端受到的支持力大小FN=18N,小滑块的落地点与B点的水平距离x=0.6m,忽略空气的阻力,取g=10m/s2,则( )
如图所示,AB为四分之一固定轨道,半径R=0.5m.一质量m=1kg的小滑块从圆弧轨道A端由静止释放,小滑块在圆弧轨道B端受到的支持力大小FN=18N,小滑块的落地点与B点的水平距离x=0.6m,忽略空气的阻力,取g=10m/s2,则( )
 如图所示,AB为四分之一固定轨道,半径R=0.5m.一质量m=1kg的小滑块从圆弧轨道A端由静止释放,小滑块在圆弧轨道B端受到的支持力大小FN=18N,小滑块的落地点与B点的水平距离x=0.6m,忽略空气的阻力,取g=10m/s2,则( )
如图所示,AB为四分之一固定轨道,半径R=0.5m.一质量m=1kg的小滑块从圆弧轨道A端由静止释放,小滑块在圆弧轨道B端受到的支持力大小FN=18N,小滑块的落地点与B点的水平距离x=0.6m,忽略空气的阻力,取g=10m/s2,则( )| A. | 小滑块到达轨道B端时的速度大小为3m/s | |
| B. | B端距水平地面的高度为0.9m | |
| C. | 小滑块由A端到B端的过程中,克服摩擦力所做的功为3J | |
| D. | 小滑块在B点处于失重状态 |
6. 电梯内放置一木块,已知木块的重力大小为G,电梯地板对木块的支持力大小为N,木块对电梯地板的压力大小为N′,支持力和压力的方向如图所示.现在电梯加速上升,则( )
电梯内放置一木块,已知木块的重力大小为G,电梯地板对木块的支持力大小为N,木块对电梯地板的压力大小为N′,支持力和压力的方向如图所示.现在电梯加速上升,则( )
 电梯内放置一木块,已知木块的重力大小为G,电梯地板对木块的支持力大小为N,木块对电梯地板的压力大小为N′,支持力和压力的方向如图所示.现在电梯加速上升,则( )
电梯内放置一木块,已知木块的重力大小为G,电梯地板对木块的支持力大小为N,木块对电梯地板的压力大小为N′,支持力和压力的方向如图所示.现在电梯加速上升,则( )| A. | N=N′>G | B. | N>N′>G | ||
| C. | 木块处于超重状态 | D. | 木块处于失重状态 |
10.一物体沿一直线运动,先后经过匀加速、匀速和匀减速运动过程,已知物体在这三个运动过程中的位移均为s,所用时间分别为2t、t和$\frac{3}{2}$t,则( )
| A. | 物体做匀加速运动时加速度大小为$\frac{s}{{t}^{2}}$ | |
| B. | 物体做匀减速运动时加速度大小为$\frac{4s}{9{t}^{2}}$ | |
| C. | 物体在这三个运动过程中的平均速度大小为$\frac{s}{3t}$ | |
| D. | 物体做匀减速运动的末速度大小为$\frac{2s}{3t}$ |
11.解决物理疑难问题的过程,往往伴随新理论的建立,在物理学史中,下列现象与物理新理论的建立不存在必然联系的是( )
| A. | 行星绕太阳运动与万有引力 | B. | 电荷间作用力与电场 | ||
| C. | 光电效应现象与光子说 | D. | 氢原子光谱与质能方程 |
 如图所示,升降机中固定一光滑斜面,倾角α=30°,斜面上弹簧的下端连接着质量m=4kg的木块,当升降机以2m/s2的加速度加速下降时(g取10m/s2).求:
如图所示,升降机中固定一光滑斜面,倾角α=30°,斜面上弹簧的下端连接着质量m=4kg的木块,当升降机以2m/s2的加速度加速下降时(g取10m/s2).求: