题目内容
【题目】如图所示,螺旋形光滑轨道竖直放置,P、Q为对应的轨道最高点,一个小球以一定速度沿轨道切线方向进入轨道,且能过轨道最高点P,则下列说法正确的是( )
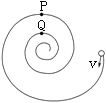
A. 小球恰能过轨道最高点P的速度为零
B. 轨道对小球不做功,小球在P点的角速度大于在Q点的角速度
C. 小球在Q点的向心加速度大于在P点的向心加速度
D. 小球在Q点对轨道的压力大于在P点对轨道的压力
【答案】CD
【解析】
小球在P点做圆周运动,重力提供向心力,故mg=![]() ,故P点速度不为零,故A错误;由于支持力始终与速度方向垂直,所以支持力不做功即轨道对小球不做功,仅有重力做功,小球机械能守恒。则P点的速度小于Q点速度,且P点的半径大于Q点的半径。所以小球通过P点的角速度小于通过Q点的。故B错误;小球在P点的速度小于Q点速度,且P点的半径大于Q点的半径。根据a=
,故P点速度不为零,故A错误;由于支持力始终与速度方向垂直,所以支持力不做功即轨道对小球不做功,仅有重力做功,小球机械能守恒。则P点的速度小于Q点速度,且P点的半径大于Q点的半径。所以小球通过P点的角速度小于通过Q点的。故B错误;小球在P点的速度小于Q点速度,且P点的半径大于Q点的半径。根据a=![]() 得,小球在P点的向心加速度小于Q点的,故C正确。小球在P点的向心加速度小于Q点的,则小球在P点的向心力小于Q点的,而向心力是由重力与轨道对它的支持力提供,因此小球在P点的支持力小于Q点的,即小球对轨道的压力P点小于Q点的。故D正确;故选CD。
得,小球在P点的向心加速度小于Q点的,故C正确。小球在P点的向心加速度小于Q点的,则小球在P点的向心力小于Q点的,而向心力是由重力与轨道对它的支持力提供,因此小球在P点的支持力小于Q点的,即小球对轨道的压力P点小于Q点的。故D正确;故选CD。

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目