题目内容
3.如图1,将一打点计时器固定在斜面上某处,打点计时器使用的交流电频率为50Hz.用米尺测得斜面的高度与长度之比为$\frac{1}{4}$.一辆质量为400g的小车拖着穿过打点计时器的纸带从斜面上滑下.图2是打出纸带的一段,相邻记数点间还有四个点未画出.由图可知,打点计时器打纸带上B点时小车的瞬时速度vB=0.15m/s,打纸带上E点时小车的瞬时速度vE=0.33m/s.小车的加速度为0.6m/s2.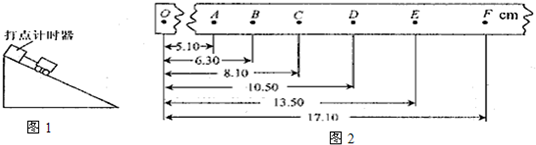
分析 能够知道相邻的计数点之间的时间间隔.纸带实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度.先根据牛顿第二定律求出阻力,根据恒力做功公式求解克服阻力所做的功.
解答 解:根据中点时刻的速度等于平均速度得:
vB=$\frac{{x}_{AC}}{2T}$=$\frac{0.081-0.051}{0.2}$m/s=0.15m/s
vE=$\frac{{x}_{DF}}{2T}$=$\frac{0.171-0.105}{0.2}$m/s=0.33m/s
根据加速度的定义式得:
a=$\frac{△v}{△t}$=$\frac{{v}_{E}-{v}_{B}}{3T}$=$\frac{0.33-0.15}{0.3}$=0.6m/s2
根据牛顿第二定律得:
mgsinθ-f=ma
解得f=$\frac{1}{4}$mg-0.6m=0.76N
所以克服阻力所做的功W=-Wf=0.76×(0.135-0.063)J=0.055J
故答案为:0.15;0.33;0.6.
点评 了解打点计时器的工作原理,清楚数据处理的方法,要注意单位的换算,难度不大,属于基础题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
13.历史上有些科学家曾把在在位移内速度变化相等的单向直线运动称为“匀变速直线运动”(现称为“另类匀变速直线运动”).“另类加速度”定义为$A=\frac{{{v_s}-{v_0}}}{S}$,其中υ0和υs分别表示某段位移s内的初速度和末速度.A>0表示物体做加速运动,A<0表示物体做减速运动.而现在物理学中加速度的定义式为:$a=\frac{{{v_t}-{v_0}}}{t}$,下列说法正确的是( )
| A. | 若A不变,则a也不变 | |
| B. | 若A不变,物体在中间位置处速度为$\frac{{{υ_0}+{υ_s}}}{2}$ | |
| C. | 若A>0且保持不变,则a逐渐增大 | |
| D. | 若A不变,物体在中间位置处速度为$\sqrt{\frac{υ_0^2+υ_s^2}{2}}$ |
18.某物体以30m/s的初速度竖直上抛,不计空气阻力,g取10m/s 2,则4s内物体的( )
| A. | 路程为65m | B. | 位移大小为25m,方向向上 | ||
| C. | 速度改变量的大小为40m/s | D. | 平均速度大小为9m/s,方向向上 |
12. 如图所示,有两根左右对称的细绳,悬挂着一个静止的物体.当两根绳子的夹角θ变大时(仍左右对称),则( )
如图所示,有两根左右对称的细绳,悬挂着一个静止的物体.当两根绳子的夹角θ变大时(仍左右对称),则( )
 如图所示,有两根左右对称的细绳,悬挂着一个静止的物体.当两根绳子的夹角θ变大时(仍左右对称),则( )
如图所示,有两根左右对称的细绳,悬挂着一个静止的物体.当两根绳子的夹角θ变大时(仍左右对称),则( )| A. | 两绳子所受的拉力都不变 | B. | 两绳子所受的拉力将同时减少 | ||
| C. | 两绳子所受的拉力将同时增大 | D. | 两绳子所受的拉力的合力将变大 |
14.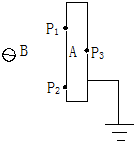 金属板A一侧接地,在其表面 上三个点P1、P2、P3,左侧附近放一个带负电的固定小球B,如图所示,则以下判断正确的是( )
金属板A一侧接地,在其表面 上三个点P1、P2、P3,左侧附近放一个带负电的固定小球B,如图所示,则以下判断正确的是( )
 金属板A一侧接地,在其表面 上三个点P1、P2、P3,左侧附近放一个带负电的固定小球B,如图所示,则以下判断正确的是( )
金属板A一侧接地,在其表面 上三个点P1、P2、P3,左侧附近放一个带负电的固定小球B,如图所示,则以下判断正确的是( )| A. | P1、P2两点左侧邻近处场强相同 | |
| B. | P1、P2两点左侧邻近处场强方向相同 | |
| C. | P1、P2处有感应电荷 | |
| D. | P3处无感应电荷 |
 如图所示,金属杆ab、cd置于平行轨道MN、PQ上,可沿轨道滑动,两轨道间距l=0.5m,轨道所在空间有垂直于轨道平面匀强磁场,磁感强度B=0.5T,用力F=0.25N向右水平拉杆ab,若ab、cd与轨道间的滑动摩擦力f1=0.15N、f2=0.1N,两杆的电阻分别为R1=R2=0.1Ω,设导轨电阻不计,ab、cd的质量关系为2m1=3m2;且ab、cd与轨道间的最大静摩擦力与滑动摩擦力相等.
如图所示,金属杆ab、cd置于平行轨道MN、PQ上,可沿轨道滑动,两轨道间距l=0.5m,轨道所在空间有垂直于轨道平面匀强磁场,磁感强度B=0.5T,用力F=0.25N向右水平拉杆ab,若ab、cd与轨道间的滑动摩擦力f1=0.15N、f2=0.1N,两杆的电阻分别为R1=R2=0.1Ω,设导轨电阻不计,ab、cd的质量关系为2m1=3m2;且ab、cd与轨道间的最大静摩擦力与滑动摩擦力相等.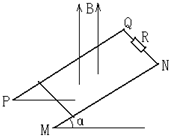 如图所示,两根平行光滑金属导轨PQ和MN相距d=0.5m,它们与水平方向的倾角为α(sinα=0.6),导轨的上方跟电阻R=4Ω相连,导轨上放一个金属棒,金属棒的质量为m=0.2kg、电阻为r=2Ω.整个装置放在方向竖直向上的匀强磁场中,磁感应强度B=1.2T.金属棒在沿斜面方向向上的恒力作用下由静止开始沿斜面向上运动,电阻R消耗的最大电功率P=1W.(g=10m/s2)求:
如图所示,两根平行光滑金属导轨PQ和MN相距d=0.5m,它们与水平方向的倾角为α(sinα=0.6),导轨的上方跟电阻R=4Ω相连,导轨上放一个金属棒,金属棒的质量为m=0.2kg、电阻为r=2Ω.整个装置放在方向竖直向上的匀强磁场中,磁感应强度B=1.2T.金属棒在沿斜面方向向上的恒力作用下由静止开始沿斜面向上运动,电阻R消耗的最大电功率P=1W.(g=10m/s2)求: