题目内容
8.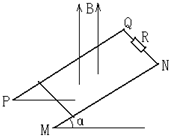 如图所示,两根平行光滑金属导轨PQ和MN相距d=0.5m,它们与水平方向的倾角为α(sinα=0.6),导轨的上方跟电阻R=4Ω相连,导轨上放一个金属棒,金属棒的质量为m=0.2kg、电阻为r=2Ω.整个装置放在方向竖直向上的匀强磁场中,磁感应强度B=1.2T.金属棒在沿斜面方向向上的恒力作用下由静止开始沿斜面向上运动,电阻R消耗的最大电功率P=1W.(g=10m/s2)求:
如图所示,两根平行光滑金属导轨PQ和MN相距d=0.5m,它们与水平方向的倾角为α(sinα=0.6),导轨的上方跟电阻R=4Ω相连,导轨上放一个金属棒,金属棒的质量为m=0.2kg、电阻为r=2Ω.整个装置放在方向竖直向上的匀强磁场中,磁感应强度B=1.2T.金属棒在沿斜面方向向上的恒力作用下由静止开始沿斜面向上运动,电阻R消耗的最大电功率P=1W.(g=10m/s2)求:(1)恒力的大小;
(2)恒力做功的最大功率.
分析 (1)由导体切割磁感线公式及功率公式可确定金属棒的最大速度;则可由F=BIL求得安培力的大小;再由平衡条件可求得恒力F的大小;
(2)由P=FV可求得最大功率.
解答 解:(1)当感应电动势为E时,回路中的总电功率为:
P=$\frac{{E}^{2}}{R+r}$
此时R上的电功率PR=($\frac{E}{R+r}$)2R
故回路中最大的电功率Pm=P•$\frac{R+r}{R}$=$\frac{3}{2}$W
因为Em=$\sqrt{{P}_{m}(R+r)}$=3V
又Em=Bdvmcos 37°
可得:金属棒滑行的最大速度vm=6.25m/s
金属棒达到最大速度时,受力情况如图乙所示.由平衡条件得:
F=mgsin α+F安cos α
其中F安=$\frac{{B}^{2}{d}^{2}{v}_{m}cosα}{R+r}$
解得:F=1.44N.
(2)当金属棒达到最大速度时,恒力做功的功率最大且为:PF=F•vm=1.44×6.25=9W.
答:(1)恒力F的大小1.44N;
(2)恒力做功的功率最大为9W.
点评 本题考查导体切割磁感线规律的应用,要注意正确利用F=BIL=$\frac{{B}^{2}{L}^{2}v}{R}$进行分析运算.

练习册系列答案
相关题目
19.下列图中不表示物体做匀速直线运动的图象是( )
| A. |  | B. | 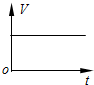 | C. |  | D. |  |
16. 三个相同的物体叠放在水平面上,B物体受到水平拉力的作用,但三个物体都处于静止状态,如图所示,下列说法正确的是( )
三个相同的物体叠放在水平面上,B物体受到水平拉力的作用,但三个物体都处于静止状态,如图所示,下列说法正确的是( )
 三个相同的物体叠放在水平面上,B物体受到水平拉力的作用,但三个物体都处于静止状态,如图所示,下列说法正确的是( )
三个相同的物体叠放在水平面上,B物体受到水平拉力的作用,但三个物体都处于静止状态,如图所示,下列说法正确的是( )| A. | A与B的接触面一定是粗糙的 | |
| B. | 各接触面都一定是粗糙的 | |
| C. | B与C,C与水平面的接触面一定是粗糙的 | |
| D. | C与水平面的接触面可能是光滑的 |
20.一质量为m的物体以初速度v0冲上一倾角为θ的光滑固定斜面,则下列说法正确的是( )
| A. | 物体做匀减速运动,其加速度的大小为gsinθ | |
| B. | 物体以速度v0匀速运动 | |
| C. | 物体从斜面底端上升到最高点所用时间为$\frac{{v}_{0}}{gcosθ}$ | |
| D. | 物体沿斜面上升的最大高度为$\frac{{{v}_{0}}^{2}}{2g}$ |
17.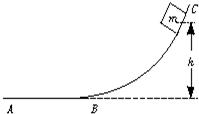 如图所示,质量为m的物体,由高h处无初速滑下,至平面上A点静止,则这个过程中各个力做功及相关能量的改变,正确的是( )
如图所示,质量为m的物体,由高h处无初速滑下,至平面上A点静止,则这个过程中各个力做功及相关能量的改变,正确的是( )
 如图所示,质量为m的物体,由高h处无初速滑下,至平面上A点静止,则这个过程中各个力做功及相关能量的改变,正确的是( )
如图所示,质量为m的物体,由高h处无初速滑下,至平面上A点静止,则这个过程中各个力做功及相关能量的改变,正确的是( )| A. | 克服重力做的功mgh | B. | 克服摩擦阻力做的功mgh | ||
| C. | 重力势能减少mgh | D. | 整个过程动能增加mgh |
19.对匀变速直线运动的特点,下列说法正确的是( )
| A. | 第1s末、2s末、3s末…的速度分别为1m/s、2m/s、3m/s…的直线运动为匀加速直线运动 | |
| B. | 匀减速直线运动中,由于加速度与初速度方向相反,则加速度为负值 | |
| C. | 物体做匀变速直线运动,其加速度是均匀变化的 | |
| D. | 在匀变速直线运动中,相同时间内速度的变化相同 |

 如图所示,质量M=10kg,上表面光滑的足够长木板在水平拉力F=50N作用下,以v0=5m/s初速度沿水平地面向右匀速运动,现有足够多的小铁块,它们质量均为m=1kg.现将一铁块无初速地放在木板最右端,当木板运动了L=1m时,又无初速地在木板最右端放上第二个铁块,只要木板运动了L就在木板最右端无初速放一铁块.求:
如图所示,质量M=10kg,上表面光滑的足够长木板在水平拉力F=50N作用下,以v0=5m/s初速度沿水平地面向右匀速运动,现有足够多的小铁块,它们质量均为m=1kg.现将一铁块无初速地放在木板最右端,当木板运动了L=1m时,又无初速地在木板最右端放上第二个铁块,只要木板运动了L就在木板最右端无初速放一铁块.求: