题目内容
14.在光滑的水平面上,用一水平拉力F使物体从静止开始移动x,平均功率为P,如果将水平拉力增加为4F,使同一物体从静止开始移动x,平均功率为( )| A. | 2P | B. | 4P | C. | 6P | D. | 8P |
分析 根据功的公式W=Fs比较拉力做功的大小,根据物体的加速度,结合位移时间公式比较运动的时间,根据功率公式P=$\frac{W}{t}$分析拉力做功功率的大小关系.
解答 解:由题知,用同一水平力F拉物体,物体运动的距离x,
根据W=Fx,
如果将水平拉力增加为4F可知:拉力做的功W2=4W1;
根据牛顿第二定律知,在光滑水平面上物体的加速度,$a=\frac{F}{m}$,所以:a2=4a1
根据x=$\frac{1}{2}a{t}^{2}$得,${t}_{2}=\frac{1}{2}{t}_{1}$
根据P=$\frac{W}{t}$得:拉力做功功率:${P}_{2}=\frac{{W}_{2}}{{t}_{2}}=\frac{4{W}_{1}}{\frac{1}{2}{t}_{1}}=8\frac{{W}_{1}}{{t}_{1}}=8{P}_{1}$.
故选:D.
点评 本题考查了学生对功的公式、功率公式的掌握和运用,比较做功大小时,紧紧抓住“力和在力的方向上移动的距离相等”,不要受接触面情况的影响.

练习册系列答案
相关题目
4.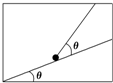 如图所示,一倾角θ=30°的光滑斜面固定在箱子底板上,一小球用一细绳拴于箱子顶部,细绳与斜面间夹角也为θ,细绳对小球的拉力为T,斜面对小球的支持力为N,重力加速度为g,小球始终相对斜面静止,则下列运动能确保T、N中只有一个为0的是( )
如图所示,一倾角θ=30°的光滑斜面固定在箱子底板上,一小球用一细绳拴于箱子顶部,细绳与斜面间夹角也为θ,细绳对小球的拉力为T,斜面对小球的支持力为N,重力加速度为g,小球始终相对斜面静止,则下列运动能确保T、N中只有一个为0的是( )
 如图所示,一倾角θ=30°的光滑斜面固定在箱子底板上,一小球用一细绳拴于箱子顶部,细绳与斜面间夹角也为θ,细绳对小球的拉力为T,斜面对小球的支持力为N,重力加速度为g,小球始终相对斜面静止,则下列运动能确保T、N中只有一个为0的是( )
如图所示,一倾角θ=30°的光滑斜面固定在箱子底板上,一小球用一细绳拴于箱子顶部,细绳与斜面间夹角也为θ,细绳对小球的拉力为T,斜面对小球的支持力为N,重力加速度为g,小球始终相对斜面静止,则下列运动能确保T、N中只有一个为0的是( )| A. | 箱子自由下落 | |
| B. | 箱子水平向右做加速运动,且加速度大小为$\frac{\sqrt{3}}{3}$g | |
| C. | 箱子水平向右做减速运动,且加速度大小为$\frac{\sqrt{3}}{3}$g | |
| D. | 箱子以任意加速度竖直向上做加速运动 |
5.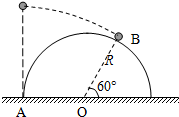 如图,一小球从一半圆轨道左端A点正上方某处开始做平抛运动(小球可视为质点),飞行过程中恰好与半圆轨道相切于B点.O为半圆轨道圆心,半圆轨道半径为R,OB与水平方向夹角为60°,重力加速度为g,则下列判断正确的是( )
如图,一小球从一半圆轨道左端A点正上方某处开始做平抛运动(小球可视为质点),飞行过程中恰好与半圆轨道相切于B点.O为半圆轨道圆心,半圆轨道半径为R,OB与水平方向夹角为60°,重力加速度为g,则下列判断正确的是( )
 如图,一小球从一半圆轨道左端A点正上方某处开始做平抛运动(小球可视为质点),飞行过程中恰好与半圆轨道相切于B点.O为半圆轨道圆心,半圆轨道半径为R,OB与水平方向夹角为60°,重力加速度为g,则下列判断正确的是( )
如图,一小球从一半圆轨道左端A点正上方某处开始做平抛运动(小球可视为质点),飞行过程中恰好与半圆轨道相切于B点.O为半圆轨道圆心,半圆轨道半径为R,OB与水平方向夹角为60°,重力加速度为g,则下列判断正确的是( )| A. | 小球抛出时的初速度为v0=$\sqrt{\frac{3gR}{2}}$ | B. | 小球抛出时的初速度为 v0=$\sqrt{\frac{3\sqrt{3}gR}{2}}$ | ||
| C. | 小球下落的高度 $h=\frac{{\sqrt{3}}}{4}R$ | D. | 小球下落的高度$h=\frac{{3\sqrt{3}}}{4}R$ |
2. 如图所示为某质点的v-t图象,向右为运动的正方向,关于这个质点在4s内的运动情况,下列说法中正确的是( )
如图所示为某质点的v-t图象,向右为运动的正方向,关于这个质点在4s内的运动情况,下列说法中正确的是( )
 如图所示为某质点的v-t图象,向右为运动的正方向,关于这个质点在4s内的运动情况,下列说法中正确的是( )
如图所示为某质点的v-t图象,向右为运动的正方向,关于这个质点在4s内的运动情况,下列说法中正确的是( )| A. | 0~2s内质点做直线运动,2~4s内质点做曲线运动 | |
| B. | 2s末质点离出发点最远 | |
| C. | 2~4s内质点的平均速度为1m/s | |
| D. | 4s末质点位于出发点左侧 |
19.下列图中不表示物体做匀速直线运动的图象是( )
| A. |  | B. | 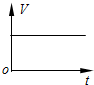 | C. |  | D. |  |
6.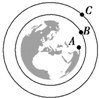 如图,物体A、B、C分别位于地球赤道、近地轨道及同步卫星轨道上,已知三个物体在共面的同心圆轨道上各自做匀速圆周运动.设V0为第一宇宙速度,g为地球表面重力加速度,T为地球自转周期,则下列判断正确的是( )
如图,物体A、B、C分别位于地球赤道、近地轨道及同步卫星轨道上,已知三个物体在共面的同心圆轨道上各自做匀速圆周运动.设V0为第一宇宙速度,g为地球表面重力加速度,T为地球自转周期,则下列判断正确的是( )
 如图,物体A、B、C分别位于地球赤道、近地轨道及同步卫星轨道上,已知三个物体在共面的同心圆轨道上各自做匀速圆周运动.设V0为第一宇宙速度,g为地球表面重力加速度,T为地球自转周期,则下列判断正确的是( )
如图,物体A、B、C分别位于地球赤道、近地轨道及同步卫星轨道上,已知三个物体在共面的同心圆轨道上各自做匀速圆周运动.设V0为第一宇宙速度,g为地球表面重力加速度,T为地球自转周期,则下列判断正确的是( )| A. | 物体A的向心加速度aA=g | B. | 三个物体的运行线速度VA>VB>VC | ||
| C. | 物体A、B、C的运行周期TC>TB>TA | D. | 物体B的环绕速度VB=V0 |
5.在地质、地震、勘探、气象和地球物理等领域的研究中,需要精确的重力加速度g值,g值可由实验精确测定,近年来测g值的一种方法叫“对称自由下落法”,它是将测g归于测长度和时间,以稳定的氦氛激光的波长为长度标准,用光学干涉的方法测距离,以铷原子钟或其他手段测时间,能将g值测得很准,具体做法是:将真空长直管沿竖直方向放置,自其中O点竖直向上抛出小球,小球又落至原处O点的时间为T2,在小球运动过程中经过比O点高H的P点,小球离开P点后又回到P点所用的时间为T1,测得T1、T2和H,可求得g等于( )
| A. | $\frac{8H}{T_2^2-T_1^2}$ | B. | $\frac{4H}{T_2^2-T_1^2}$ | C. | $\frac{8H}{{{{({T_2}-{T_1})}^2}}}$ | D. | $\frac{H}{{4{{({T_2}-{T_1})}^2}}}$ |