题目内容
15.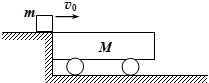 如图13所示,质量为1.6kg的平板小车静止在光滑的水平地面上,质量为0.4kg的木块以2m/s的速度滑上平板小车,木块与平板小车之间的动摩擦因数为0.2(g取10m/s2).设小车足够长.求
如图13所示,质量为1.6kg的平板小车静止在光滑的水平地面上,质量为0.4kg的木块以2m/s的速度滑上平板小车,木块与平板小车之间的动摩擦因数为0.2(g取10m/s2).设小车足够长.求(1)木块和小车相对静止时小车的速度;
(2)从木块滑上小车到它们处于相对静止时,木块相对地面滑行的位移;
(3)欲使木块不离开平板小车,则小车的长度至少为多少?
分析 (1)木块与小车组成的系统动力守恒,应用动量守恒定律可以求出小车的速度.
(2)对木块由动能定理可以求出其位移.
(3)由动能定理可以求出小车的位移,木块与小车的位移之差是小车的最小长度.
解答 解(1)对木块和小车组成的系统,从木块滑上小车到相对静止过程系统动量守恒,
以木块的初速度方向为正方向,由动量守恒定律得:mv0=(M+m)v,代入数据解得:v=0.4m/s;
(2)对木块,从开始静止到与小车相对静止过程,由动能定理得:
-fs2=$\frac{1}{2}$mv2-$\frac{1}{2}$mv02,代入数据解得:s2=0.96m;
(3)由牛顿第三定律:f=f′=μmg,
对小车,从开始静止到与木块相对静止过程,
由动能定理得:f′s1=$\frac{1}{2}$Mv2,代入数据解得:s1=0.16m,
二者的相对位移:△s=s2-s1=0.96m-0.16m=0.8m,
由此可知,小车的长度至少为0.8m;
答:(1)木块和小车相对静止时小车的速度为0.4m/s;
(2)从木块滑上小车到它们处于相对静止时,木块相对地面滑行的位移为0.96m;
(3)欲使木块不离开平板小车,则小车的长度至少为0.8m.
点评 本题考查了求速度、位移与小车长度问题,分析清楚物体运动过程是正确解题的前提与关键,应用动量守恒定律与动能定理可以解题,本题是常规题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.2014年3月8日凌晨,飞往北京的马航MH370航班起飞后与地面失去联系.我国西安卫星测控中心启动卫星测控应急预案,紧急调动海洋、风云、高分、遥感等4个型号、近10颗卫星为地面搜救行动提供技术支持.假设某颗圆周运动卫星A轨道在赤道平面内,距离地面的高度为地球半径的2.5倍,取同步卫星B离地面高度为地球半径的6倍,则( )
| A. | 卫星A的线速度大于第一宇宙速度 | |
| B. | 卫星A的向心加速度是地球表面重力加速度的$\frac{4}{49}$倍 | |
| C. | 同步卫星B的向心加速度为地球表面赤道上物体随地球自转向心加速度的$\frac{1}{49}$倍 | |
| D. | 卫星B的周期小于卫星A的周期 |
6. 质量为m的小球A被长为L的轻绳悬挂在O点,且在光滑的水平桌面上做匀速圆周运动,如图所示,当小球角速度为ω时,小球对桌面的压力恰好为零,此时轻绳与竖直方向的夹角为θ,则ω为( )
质量为m的小球A被长为L的轻绳悬挂在O点,且在光滑的水平桌面上做匀速圆周运动,如图所示,当小球角速度为ω时,小球对桌面的压力恰好为零,此时轻绳与竖直方向的夹角为θ,则ω为( )
 质量为m的小球A被长为L的轻绳悬挂在O点,且在光滑的水平桌面上做匀速圆周运动,如图所示,当小球角速度为ω时,小球对桌面的压力恰好为零,此时轻绳与竖直方向的夹角为θ,则ω为( )
质量为m的小球A被长为L的轻绳悬挂在O点,且在光滑的水平桌面上做匀速圆周运动,如图所示,当小球角速度为ω时,小球对桌面的压力恰好为零,此时轻绳与竖直方向的夹角为θ,则ω为( )| A. | $\sqrt{\frac{gcosθ}{L}}$ | B. | $\sqrt{\frac{gsinθ}{L}}$ | C. | $\sqrt{\frac{g}{Lcosθ}}$ | D. | $\sqrt{\frac{g}{Lsinθ}}$ |
10. 如图6所示,国际花样滑冰锦标赛男女双人自由滑项目中,我国著名选手申雪、赵宏博在决赛中的一个瞬间,他们正以相同的速度v0在光滑冰面上前进,当赵宏博用力将申雪向后推出后,申雪单腿沿直线匀速运动后继而做出优美的旋转动作,若赵宏博以速度大小为v向后推出申雪,则赵宏博的速度大小变为 (设赵宏博的质量为M,申雪的质量为m)( )
如图6所示,国际花样滑冰锦标赛男女双人自由滑项目中,我国著名选手申雪、赵宏博在决赛中的一个瞬间,他们正以相同的速度v0在光滑冰面上前进,当赵宏博用力将申雪向后推出后,申雪单腿沿直线匀速运动后继而做出优美的旋转动作,若赵宏博以速度大小为v向后推出申雪,则赵宏博的速度大小变为 (设赵宏博的质量为M,申雪的质量为m)( )
 如图6所示,国际花样滑冰锦标赛男女双人自由滑项目中,我国著名选手申雪、赵宏博在决赛中的一个瞬间,他们正以相同的速度v0在光滑冰面上前进,当赵宏博用力将申雪向后推出后,申雪单腿沿直线匀速运动后继而做出优美的旋转动作,若赵宏博以速度大小为v向后推出申雪,则赵宏博的速度大小变为 (设赵宏博的质量为M,申雪的质量为m)( )
如图6所示,国际花样滑冰锦标赛男女双人自由滑项目中,我国著名选手申雪、赵宏博在决赛中的一个瞬间,他们正以相同的速度v0在光滑冰面上前进,当赵宏博用力将申雪向后推出后,申雪单腿沿直线匀速运动后继而做出优美的旋转动作,若赵宏博以速度大小为v向后推出申雪,则赵宏博的速度大小变为 (设赵宏博的质量为M,申雪的质量为m)( )| A. | $\frac{m}{M}$(v0+v) | B. | $\frac{m}{M}$(v0-v) | C. | M+$\frac{m}{M}$(v0-v) | D. | M-$\frac{m}{M}$(v0-v) |
20. 如图所示,A、B为两个固定的等量的同种正点电荷,在它们连线的中点处有一个可以自由运动的正点电荷C,现给电荷C一个垂直于连线的初速度vc,若不计电荷C所受的重力,则关于电荷C运动过程中的速度和加速度情况,下列说法正确的是( )
如图所示,A、B为两个固定的等量的同种正点电荷,在它们连线的中点处有一个可以自由运动的正点电荷C,现给电荷C一个垂直于连线的初速度vc,若不计电荷C所受的重力,则关于电荷C运动过程中的速度和加速度情况,下列说法正确的是( )
 如图所示,A、B为两个固定的等量的同种正点电荷,在它们连线的中点处有一个可以自由运动的正点电荷C,现给电荷C一个垂直于连线的初速度vc,若不计电荷C所受的重力,则关于电荷C运动过程中的速度和加速度情况,下列说法正确的是( )
如图所示,A、B为两个固定的等量的同种正点电荷,在它们连线的中点处有一个可以自由运动的正点电荷C,现给电荷C一个垂直于连线的初速度vc,若不计电荷C所受的重力,则关于电荷C运动过程中的速度和加速度情况,下列说法正确的是( )| A. | 加速度始终增大 | B. | 加速度先增大后减小 | ||
| C. | 速度先增大后减小 | D. | 速度一直减小 |
7.关于功和功率的计算,下列说法中正确的是( )
| A. | 用W=Fxcosθ可以计算变力做功 | B. | 用W合=Ek2-Ek1可以计算变力做功 | ||
| C. | 用W=Pt只能计算恒力做功 | D. | 用P=$\frac{W}{t}$可以计算瞬时功率 |
4.工程师驾驶同一辆汽车以额定功率在A、B两种不同的路面上进行性能测试.汽车在路面A、B受到的阻力分别为fA、fB(fA>fB),最大速度分别为vA、vB,达到最大速度时的牵引力分别为FA、FB,则( )
| A. | vA<vB | B. | vA>vB | C. | FA=FB | D. | FA<FB |

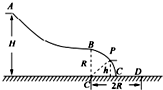 图为某游乐场内水上滑梯轨道示意图,整个轨道在同一竖直平面内,表面粗糙的AB段轨道与四分之一光滑圆弧轨道BC在B点水平相切,点A距水面的高度为H,圆弧轨道BC的半径为R.圆心O恰在水面,一质量为m的游客(视为质点)可从轨道AB上任意位置滑下,不计空气阻力.
图为某游乐场内水上滑梯轨道示意图,整个轨道在同一竖直平面内,表面粗糙的AB段轨道与四分之一光滑圆弧轨道BC在B点水平相切,点A距水面的高度为H,圆弧轨道BC的半径为R.圆心O恰在水面,一质量为m的游客(视为质点)可从轨道AB上任意位置滑下,不计空气阻力.