题目内容
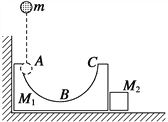
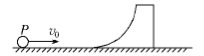
【题目】如图所示,AB为竖直平面内的细管状半圆轨道,AB连线为竖直直径,轨道半径R=6.4m,轨道内壁光滑,A、B两端为轨道的开口。BC为粗糙水平轨道,其长度s=8.4m。CD为倾角θ=37°的斜面。用两个小物块a、b紧靠在一轻弹簧的两端将弹簧压缩,用细线将两物块绑住,沿轨道静置于C点。弹簧很短,物块与弹簧均不拴接,物块a的线度略小于细管的内径。烧断细线,两物块先后落到斜面的M点,CM两点之间的距离L=12m。已知物块跟水平轨道之间的动摩擦因数![]() ,忽略空气阻力,取重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8。求:
,忽略空气阻力,取重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8。求:
(1)物块b刚离开弹簧的瞬间,其速率v0是多少;
(2)设物块a、b的质量分别为m1、m2,则![]() 是多少?(结果可以用根式表示)
是多少?(结果可以用根式表示)
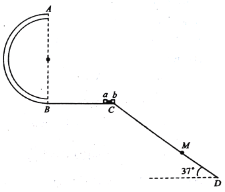
【答案】(1)![]() ; (2)
; (2)![]() 或
或![]()
【解析】
(1)物块b离开弹簧后做平抛运动。设从C运动到M历时为t,则
![]() ,
,![]()
代入数据解得
![]() ,
,![]()
(2) ①物块a能够经过A点做平抛运动落到斜面的M点。设物块a经过A点的速率为vA,从A运动到M历时为t1,则
![]() ,
,![]()
解得
![]() ,
,![]()
设物块a刚被弹簧弹开时的速率为vCl,在从C运动到A的过程中,由动能定理得
![]()
解得
vCl=19m/s
弹簧弹开物块a、b的过程中,物块a、b动量守恒。选向右的方向为正方向,由动量守恒定律得
![]()
解得
![]()
②物块a被弹簧弹开后不能到达A点,物块a从C点做平抛运动落到斜面的M点,做平抛运动的初速度大小也是v0。设物块a刚被弹簧弹开时的速率为vC2,在物块a从C向左运动到再次回到C点的过程中,由动能定理得
![]()
解得:
![]()
弹簧弹开物块a、b的过程中,物块a、b动量守恒。选向右的方向为正方向,由动量守恒定律得
![]()
解得

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目