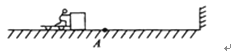Question

【题目】(18分)如图所示，在高出水平地面h＝1.8 m的光滑平台上放置一质量M＝2 kg、由两种不同材料连接成一体的薄板A，其右段长度l1＝0.2 m且表面光滑，左段表面粗糙．在A最右端放有可视为质点的物块B，其质量m＝1 kg，B与A左段间动摩擦因数μ＝0.4.开始时二者均静止，现对A施加F＝20 N水平向右的恒力，待B脱离A（A尚未露出平台）后，将A取走．B离开平台后的落地点与平台右边缘的水平距离x＝1.2 m．（取g＝10 m/s2）求：

（1）B离开平台时的速度vB.

（2）B从开始运动到刚脱离A时，B运动的时间tB和位移xB.

（3）A左段的长度l2.

Answer 1

【答案】（1）2m/s（2）0.5s, 0.5m（3）1.5m

【解析】

试题分析：（1）设物块平抛运动的时间为t，由平抛运动规律得：h=gt2，x=vBt

联立解得vB=2m/s．

（2）设B的加速度为aB，B在A的粗糙表面滑动，受向右的滑动摩擦力做匀加速直线运动．

由牛顿第二定律，F合=μmg=maB，

由匀变速直线运动规律，vB=aBtB，xB=aBtB 2，

联立解得：tB=0.5s，xB=0.5m．

（3）设B刚好开始运动时A的速度为v，以A为研究对象，由动能定理得Fl1=Mv12

设B运动后A的加速度为aA，由牛顿第二定律和运动学的知识得：

F-μmg=MaA，（l2+xB）=v1tB+aAtB 2，

联立解得l2=1.5m．