题目内容
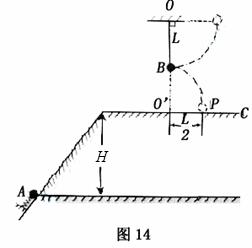
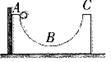
如图,长为l=0.5m的细绳,上端固定于O点,下端悬挂质量为M=0.99kg的沙箱。一颗质量为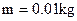 的子弹,以
的子弹,以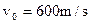 的水平速度射入沙箱并留在其中。
的水平速度射入沙箱并留在其中。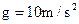 。求:
。求:
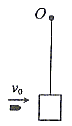
(1)子弹和沙箱开始做圆周运动的初速度v;
(2)子弹打入沙箱的过程中产生的内能E;
(3)子弹和沙箱能否通过圆周的最高点?
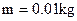 的子弹,以
的子弹,以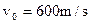 的水平速度射入沙箱并留在其中。
的水平速度射入沙箱并留在其中。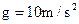 。求:
。求:
(1)子弹和沙箱开始做圆周运动的初速度v;
(2)子弹打入沙箱的过程中产生的内能E;
(3)子弹和沙箱能否通过圆周的最高点?
(1)6.0m/s (2)1782J (3)能通过
(1)以子弹和沙箱为研究对象,由动量守恒定律
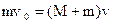 (3分)
(3分)
求出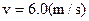 (2分)
(2分)
(2)由能量守恒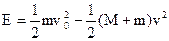 (3分)
(3分)
求出E=1782(J) (2分)
(3)设子弹和沙箱能到达圆周最高点需要的最小速度为vmin
此时重力提供向心力
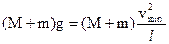 (2分)
(2分)
求出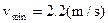 (1分)
(1分)
设子弹和沙箱能到达圆周最高点,到达最高点的速度为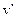
由机械能守恒定律
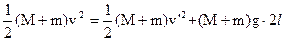 (2分)
(2分)
求出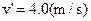 (1分)
(1分)
因为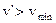
所以子弹和沙箱能通过圆周的最高点(2分)
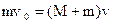 (3分)
(3分)求出
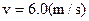 (2分)
(2分)(2)由能量守恒
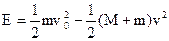 (3分)
(3分)求出E=1782(J) (2分)
(3)设子弹和沙箱能到达圆周最高点需要的最小速度为vmin
此时重力提供向心力
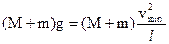 (2分)
(2分)求出
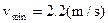 (1分)
(1分)设子弹和沙箱能到达圆周最高点,到达最高点的速度为
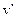
由机械能守恒定律
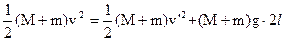 (2分)
(2分)求出
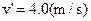 (1分)
(1分)因为
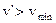
所以子弹和沙箱能通过圆周的最高点(2分)

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目