题目内容
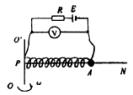
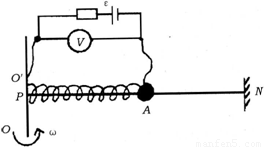
某同学利用业余时间为工厂设计了一个测定机器转动角速度的装置,如图所示.A为一金属小球,质量为m,电阻不计.水平光滑的均匀滑杆PN由合金材料制成,电阻不能忽略,PA与电路相连接,电源电动势为ε,内阻不计,限流电阻与杆PN的总电阻相等.连接小球的弹簧,由绝缘材料制成,弹簧的劲度系数为K.小球静止时恰好在滑杆PN的中点,当系统绕OO′轴匀速转动时,电压表的示数为U,试求此时系统转动的角速度ω.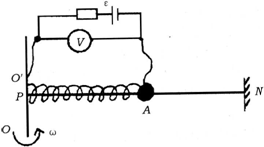

设杆PN电阻为R0,系统转动时杆PA段的电阻为R
根据欧姆定律得:
U1=
?
R0=
ε (1)
U2=
?R (2)
设弹簧原长为l,则实际长度l0(反映PN杆接入电路中的长度)为:
l0=
?2l (3)
弹簧伸长量为:
x=l0-l (4)
据胡克定律和牛顿第二定律得 Kx=mω2l (5)
由(1)(2)(3)(4)(5)式解得:
ω=
(6)
答:此时系统转动的角速度ω为
.
根据欧姆定律得:
U1=
| ε | ||
R0+
|
| 1 |
| 2 |
| 1 |
| 3 |
U2=
| ε |
| R0+R |
设弹簧原长为l,则实际长度l0(反映PN杆接入电路中的长度)为:
l0=
| R |
| R0 |
弹簧伸长量为:
x=l0-l (4)
据胡克定律和牛顿第二定律得 Kx=mω2l (5)
由(1)(2)(3)(4)(5)式解得:
ω=
|
答:此时系统转动的角速度ω为
|

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
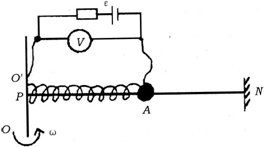 (2003?烟台模拟)某同学利用业余时间为工厂设计了一个测定机器转动角速度的装置,如图所示.A为一金属小球,质量为m,电阻不计.水平光滑的均匀滑杆PN由合金材料制成,电阻不能忽略,PA与电路相连接,电源电动势为ε,内阻不计,限流电阻与杆PN的总电阻相等.连接小球的弹簧,由绝缘材料制成,弹簧的劲度系数为K.小球静止时恰好在滑杆PN的中点,当系统绕OO′轴匀速转动时,电压表的示数为U,试求此时系统转动的角速度ω.
(2003?烟台模拟)某同学利用业余时间为工厂设计了一个测定机器转动角速度的装置,如图所示.A为一金属小球,质量为m,电阻不计.水平光滑的均匀滑杆PN由合金材料制成,电阻不能忽略,PA与电路相连接,电源电动势为ε,内阻不计,限流电阻与杆PN的总电阻相等.连接小球的弹簧,由绝缘材料制成,弹簧的劲度系数为K.小球静止时恰好在滑杆PN的中点,当系统绕OO′轴匀速转动时,电压表的示数为U,试求此时系统转动的角速度ω.