题目内容
7. 如图所示是位于X星球表面的竖直光滑圆弧轨道,宇航员实验发现,当位于轨道最低点的小球速度至少为v0时,才能在竖直面内做完整的圆周运动.已知圆弧轨道半径为r,X星球的半径为R,万有引力常量为G.求:(结果可以用根式表示)
如图所示是位于X星球表面的竖直光滑圆弧轨道,宇航员实验发现,当位于轨道最低点的小球速度至少为v0时,才能在竖直面内做完整的圆周运动.已知圆弧轨道半径为r,X星球的半径为R,万有引力常量为G.求:(结果可以用根式表示)(1)X星球表面重力加速度;
(2)X星球的第一宇宙速度;
(3)环绕X星球的轨道半径为2R的卫星的周期.
分析 (1)小球刚好能在竖直面内做完整的圆周运动,有重力充当向心力,小球在光滑圆弧轨道运动的过程中,只有重力做功,机械能守恒,根据机械能守恒得出重力加速度的大小.
(2)根据万有引力提供向心力,以及万有引力等于重力,求第一宇宙速度
(3)根据万有引力提供向心力,以及万有引力等于重力,联立解出环月卫星的周期
解答 解:( 1)设X星球表面重力加速度为g,质量为M,小球刚好能做完整的圆周运动;则小球在最高点时,仅由重力提供向心力;根据牛顿第二定律有:
mg=$m\frac{{V}^{2}}{r}$
小球从轨道最低点到最高点的过程中,由动能定理有:
-mg×$2r=\frac{1}{2}m{v}^{2}-\frac{1}{2}m{V}_{0}^{2}$
联立两式可得:g=$\frac{{V}_{0}^{2}}{5r}$
(2)在X星球发射卫星的最小速度为月球第一宇宙速度
$\frac{GM{m}_{1}}{{R}^{2}}={m}_{1}\frac{{V}_{min}^{2}}{R}$
又$\frac{GM{m}_{2}}{{R}^{2}}={m}_{2}g$
联立方程解得:Vmin=${V}_{0}\sqrt{\frac{R}{5r}}$
(3)环绕X星球的轨道半径为2R的卫星由万有引力提供向心力,有
$\frac{GMm}{4{R}^{2}}=m\frac{4{π}^{2}}{{T}^{2}}2R$
解得T=$4πR\sqrt{\frac{R}{GM}}$$•\sqrt{2}$=$4π\sqrt{\frac{R}{g}}$=$\frac{4π}{{V}_{0}}\sqrt{10Rr}$
答:(1)X星球表面重力加速度$\frac{{V}_{0}^{2}}{5r}$;
(2)X星球的第一宇宙速度${V}_{0}\sqrt{\frac{R}{5r}}$;
(3)环绕X星球的轨道半径为2R的卫星的周期$\frac{4π}{{V}_{0}}\sqrt{10Rr}$
点评 解决本题的关键会运用机械能守恒定律定律解题,知道小球在内轨道运动恰好过最高点的临界条件.以及掌握万有引力提供向心力和万有引力等于重力

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{h}{υ}$ | B. | $\frac{υ}{g}$ | C. | $\frac{2h}{υ}$ | D. | $\frac{2υ}{g}$ |
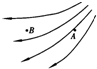
| A. | A点的电场强度较大 | |
| B. | 因为B点没有电场线,所以电荷在B点不受到电场力作用 | |
| C. | 同一点电荷放在A点受到的电场力比放在B点时受到的电场力大 | |
| D. | 正电荷放在A点由静止释放,电场线就是它的运动轨迹 |
 小球从静上开始沿固定圆环做圆周运动,其运动的速度大小与时间成正比,若小球做圆周运动第一周的时间为T,则小球做圆周运动第二周的时间为( )
小球从静上开始沿固定圆环做圆周运动,其运动的速度大小与时间成正比,若小球做圆周运动第一周的时间为T,则小球做圆周运动第二周的时间为( )| A. | $\frac{1}{2}$T | B. | ($\sqrt{2}$-1)T | C. | ($\sqrt{3}$-$\sqrt{2}$)T | D. | $\frac{1}{4}$T |
| A. | 牛顿在发现万有引力定律的过程中应用到了牛顿第二定律和牛顿第三定律 | |
| B. | 亚里士多德通过实验研究和逻辑推理认为:自由落体运动是匀加速直线运动 | |
| C. | 哥白尼提出了日心说并发现了行星沿椭圆轨道运行的规律 | |
| D. | 牛顿在伽利略和笛卡尔研究成果的基础上提出了牛顿第一定律 |
 一汽缸竖直放在水平地面上,缸体质量M=10kg,活塞质量m=4kg,活塞横截面积S=2×10-3 m2,活塞上面的汽缸内封闭了一定质量的理想气体,下面有气孔O与外界相通,大气压强p0=10×105Pa.活塞下面与劲度系数k=2×103 N/m的轻弹簧相连.当汽缸内气体温度为127℃时弹簧为自然长度,此时缸内气柱长度L1=20cm,g取10m/s2,活塞不漏气且与缸壁无摩擦.当缸内气柱长度L2=24cm时,缸内气体温度为多少K?
一汽缸竖直放在水平地面上,缸体质量M=10kg,活塞质量m=4kg,活塞横截面积S=2×10-3 m2,活塞上面的汽缸内封闭了一定质量的理想气体,下面有气孔O与外界相通,大气压强p0=10×105Pa.活塞下面与劲度系数k=2×103 N/m的轻弹簧相连.当汽缸内气体温度为127℃时弹簧为自然长度,此时缸内气柱长度L1=20cm,g取10m/s2,活塞不漏气且与缸壁无摩擦.当缸内气柱长度L2=24cm时,缸内气体温度为多少K? 如图所示,圆柱形气缸倒置在水平粗糙地面上,内封一定质量的空气,气缸质量为M=10kg,活塞质量为m=5kg,截面积为S=20cm2,活塞与缸壁的摩擦不计,缸壁厚度不计.当缸内气体温度为t1=27℃时,活塞刚好与地面相接触,但对地面无压力.现使缸内气体温度缓慢升高,当气缸(不含活塞)恰好对地面无压力时,求缸内气体的温度.大气压强为Po=1.0×105Pa,重力加速度g=10m/s2.
如图所示,圆柱形气缸倒置在水平粗糙地面上,内封一定质量的空气,气缸质量为M=10kg,活塞质量为m=5kg,截面积为S=20cm2,活塞与缸壁的摩擦不计,缸壁厚度不计.当缸内气体温度为t1=27℃时,活塞刚好与地面相接触,但对地面无压力.现使缸内气体温度缓慢升高,当气缸(不含活塞)恰好对地面无压力时,求缸内气体的温度.大气压强为Po=1.0×105Pa,重力加速度g=10m/s2.