题目内容
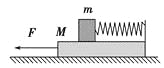
【题目】质量mB=1 kg的小物块B以初速度v0=6 m/s滑上一静止放在光滑水平面上的木板A的左端,已知木板的质量为mA=2 kg,当A向右运动的位移为L=0.5 m时,B的速度为vB=4 m/s,此时A的右端与固定竖直挡板相距x,已知木板A足够长(保证B始终不从A上滑出),A与挡板碰撞无机械能损失,A、B之间动摩擦因数为μ=0.2,g取10 m/s2,求:当x满足什么条件时,A与竖直挡板只能发生一次碰撞?
![]()
【答案】x≥0.625 m
【解析】
要使A与竖直挡板只能发生一次碰撞,A与挡板碰撞后,A的动量大于B的动量。对A与挡板碰撞前的过程,由动量守恒定律列式,得到A、B与挡板碰前瞬间的速度,以A为研究对象,运用动能定理列式。
设A、B与挡板碰前瞬间的速度分别为vA1、vB1,取向右为正方向,
由动量守恒定律得:mBv0=mAvA1+mBvB1
以A为研究对象,由动能定理得:![]()
由于A与挡板碰撞无机械能损失,故A与挡板碰后瞬间的速度大小为vA1,碰后系统总动量不再向右时,A与竖直挡板只能发生一次碰撞,即mAvA1≥mBvB1
联立解得x≥0.625 m

练习册系列答案
相关题目