��Ŀ����
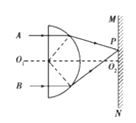
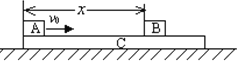
����Ŀ����ͼ��ʾ��CDEΪ�⻬�Ĺ��������ED��ˮƽ�ģ�CD����ֱƽ���ڵİ�Բ����ED������D�㣬�Ұ뾶R=0��5m������m=0��1kg�Ļ���A��ֹ��ˮƽ����ϣ���һ����M=0��5kg�Ļ���Bǰ��װ��һ���ʵ��ɣ�A��B������Ϊ�ʵ㣩���ٶ�v0�����˶����뻬��A����������������������A�ܹ���Բ��ߵ�C��ȡ�������ٶ�g=10m/s2����
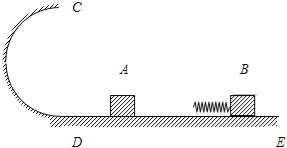
��1��B��������Ҫ�Զ���ٶ���ǰ�˶���
��2���������Aǡ���ܹ�C�㣬����B�뻬��A���������ʵ��ɵ����������Ϊ���٣�
���𰸡���1��3m/s ��2��0��375J
�������������������ţ�ٵڶ������������A��������ߵ���ٶȣ���ײ����ϵͳ�����غ㡢��е���غ㣬Ӧ�ö����غ㶨�����е���غ㶨�ɿ������B�ij��ٶȣ���ײ�������ٶ����ʱ����ѹ������������������ײ����ϵͳ�����غ㡢��е���غ㣬Ӧ�ö����غ㶨�����е���غ㶨�ɿ�����������������
�軬��A��C��ʱ�ٶ�ΪvC��B��A��ײ��B��A���ٶȷֱ�Ϊv1��v2��
B��ײǰ���ٶ�Ϊv0����Բ�����ߵ���ٽ������������ṩ������
��ţ�ٵڶ����ɵ��� ![]()
�ɻ�е���غ㶨�ɵ�![]()
B��A����������ײ����ײ���̶����غ㡢��е���غ㣬������Ϊ�������ɶ����غ㶨�ɵ� Mv0��Mv1��mv2
�ɻ�е���غ㶨�ɵ� ![]()
���v0��3 m/s.
B��A��ײ�������ٶ���ͬʱ���������������Ep���蹲ͬ�ٶ�Ϊv��
A��B��ײ����ϵͳ�����غ㡢��е���غ㣬
������Ϊ�������ɶ����غ㶨�ɵ�:Mv0��(M��m)v
�ɻ�е���غ㶨�ɵ� ![]()
�������Ep��0.375 J.

 ����ͬ�����Ծ�ϵ�д�
����ͬ�����Ծ�ϵ�д�