题目内容
如图甲所示，质量为m=50g，长l=10cm的铜棒，用长度亦为l的两根轻软导线水平悬吊在竖直向上的匀强磁场中，磁感应强度B=
T．未通电时，轻线在竖直方向，通入恒定电流后，棒向外偏转的最大角度θ=37°，求此棒中恒定电流的大小．
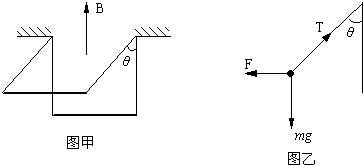
某同学的解法如下：对铜棒进行受力分析，通电时导线向外偏转，说明安培力方向垂直电流和磁场方向向外，受力如图乙所示（侧视图）．
当最大偏转角θ=37°时，棒受力平衡，有：tanθ=
=
∴I=
=
A=11.25A
请你判断，他的解法是否正确？如果错误的，请指出错在哪里，并且将做出正确的解法．
| 1 |
| 3 |
某同学的解法如下：对铜棒进行受力分析，通电时导线向外偏转，说明安培力方向垂直电流和磁场方向向外，受力如图乙所示（侧视图）．
当最大偏转角θ=37°时，棒受力平衡，有：tanθ=
| F |
| mg |
| BIL |
| mg |
∴I=
| mgtanθ |
| BL |
0.05×10×
| ||
|
请你判断，他的解法是否正确？如果错误的，请指出错在哪里，并且将做出正确的解法．
分析：该同学的解法，将偏转最大角度当作平衡状态是错误的．可根据动能定理或将此摆与单摆类比，运用对称性求解．
解答：解：不正确．错误原因：认为棒到达最高点速度为零时，一定处于平衡状态；或者认为偏角最大的位置是平衡位置．
正确的解法是：铜棒受到的安培力为 F1=BIl
解法一 根据动能定理得
BIl?lsinθ-mgl（1-cosθ）=0
解得，I=
=
=5A
解法二：由于mg与FI都是大小、方向恒定，mg与FI合力也是恒力，可
类比于重力，它的平衡位置与竖直方向成
角度，从受力分析得到
=tg
解得，I=
=
=5A
答：他的解法不正确，错误原因：认为棒到达最高点速度为零时，一定处于平衡状态；或者认为偏角最大的位置是平衡位置．正确的解法如上所示，结果是此棒中恒定电流的大小是5A．
正确的解法是：铜棒受到的安培力为 F1=BIl
解法一 根据动能定理得
BIl?lsinθ-mgl（1-cosθ）=0
解得，I=
| mg(1-cosθ) |
| Blsinθ |
| 0.05×10×(1-0.8) | ||
|
解法二：由于mg与FI都是大小、方向恒定，mg与FI合力也是恒力，可
类比于重力，它的平衡位置与竖直方向成
| θ |
| 2 |
| F1 |
| mg |
| θ |
| 2 |
解得，I=
mgtg
| ||
| BL |
| mg(1-cosθ) |
| BLsinθ |
答：他的解法不正确，错误原因：认为棒到达最高点速度为零时，一定处于平衡状态；或者认为偏角最大的位置是平衡位置．正确的解法如上所示，结果是此棒中恒定电流的大小是5A．
点评：考查学生观察是否细仔，最大偏角与平衡状态的关系，同时还体现如何正确求功．
练习册系列答案
冲刺100分1号卷系列答案
相关题目
如图甲所示，质量为m=1kg的物体置于倾角为θ=37°固定斜面上（斜面足够长），对物体施加平行于斜面向上的恒力F，作用时间t1=1s时撤去拉力，物体运动的部分v-t图象如图乙所示，取g=10m/s2．试求：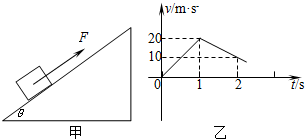
如图甲所示，质量为m=1kg的物体置于倾角为θ=37°的固定且足够长的斜面上，对物体施以平行于斜面向上的拉力F，t1=1s时撤去拉力，物体运动的部分v-t图象如图乙所示．试求：
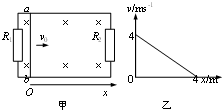如图甲所示，质量为m=0.5kg、电阻r=1Ω的跨接杆ab可以无摩擦地沿水平固定导轨滑行，导轨足够长，两导轨间宽度为L=1m，导轨电阻不计，电阻R1=1.5Ω，R2=3Ω，装置处于竖直向下的匀强磁场中，磁感应强度为B=1T．杆从x轴原点O以水平初速度向右滑行，直到停止．已知杆在整个运动过程中v随位移x变化的关系如图乙所示．求：