题目内容
如图甲所示,质量为m=5g,长l=10cm的铜棒,用长度亦为l的两根轻软导线水平悬吊在竖直向上的匀强磁场中,磁感应强度B=
T.未通电时,轻线在竖直方向,通入恒定电流后,棒向外偏转的最大角度θ=53°,求此棒中恒定电流的大小.
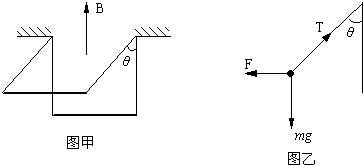
某同学的解法如下:对铜棒进行受力分析,通电时导线向外偏转,说明安培力方向垂直电流和磁场方向向外,受力如图乙所示(侧视图).
当最大偏转角θ=53°时,棒受力平衡,有:tanθ=
=
I=
=
=20A
(1)请你判断,他的解法是否正确?错误的请指出错误所在,并改正.
(2)此棒的最大动能是多少?
| 1 |
| 3 |

某同学的解法如下:对铜棒进行受力分析,通电时导线向外偏转,说明安培力方向垂直电流和磁场方向向外,受力如图乙所示(侧视图).
当最大偏转角θ=53°时,棒受力平衡,有:tanθ=
| F |
| mg |
| BIl |
| mg |
| mgtanθ |
| Bl |
0.005×10×
| ||
|
(1)请你判断,他的解法是否正确?错误的请指出错误所在,并改正.
(2)此棒的最大动能是多少?
分析:根据动能定理可以求得电流的大小,当速度最大时,导体棒受力平衡,有动能定理求得最大的动能.
解答:解:(1)此同学的解法不正确,最大偏转角θ=53°时棒不处于平衡状态.而是速度为零.
正确的解法为:
由动能定理得:BIl?lsin53°-mgl(1-cos53°)=0
I=
=
=0.75A
(2)设偏转角为β时,当速度方向上的合力为零时,棒的动能最大.
即tanβ=
=
时,
由动能定理得:BIl?lsinβ-mgl(1-cosβ)=Ek-0
解得:EK=6×10-4J
正确的解法为:
由动能定理得:BIl?lsin53°-mgl(1-cos53°)=0
I=
| mg(1-cos530) |
| Blsin530 |
| 0.005×10×(1-0.6) | ||
|
(2)设偏转角为β时,当速度方向上的合力为零时,棒的动能最大.
即tanβ=
| BIl |
| mg |
| 1 |
| 2 |
由动能定理得:BIl?lsinβ-mgl(1-cosβ)=Ek-0
解得:EK=6×10-4J
点评:最大偏转角θ=53°时棒不处于平衡状态.而是速度为零,这是这类题目中经常出现的错误,在解题的时候一定要注意.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图甲所示,质量为m=1kg的物体置于倾角为θ=37°固定斜面上(斜面足够长),对物体施加平行于斜面向上的恒力F,作用时间t1=1s时撤去拉力,物体运动的部分v-t图象如图乙所示,取g=10m/s2.试求:
如图甲所示,质量为m=1kg的物体置于倾角为θ=37°固定斜面上(斜面足够长),对物体施加平行于斜面向上的恒力F,作用时间t1=1s时撤去拉力,物体运动的部分v-t图象如图乙所示,取g=10m/s2.试求: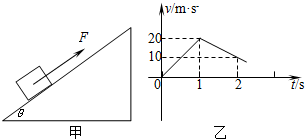 如图甲所示,质量为m=1kg的物体置于倾角为θ=37°的固定且足够长的斜面上,对物体施以平行于斜面向上的拉力F,t1=1s时撤去拉力,物体运动的部分v-t图象如图乙所示.试求:
如图甲所示,质量为m=1kg的物体置于倾角为θ=37°的固定且足够长的斜面上,对物体施以平行于斜面向上的拉力F,t1=1s时撤去拉力,物体运动的部分v-t图象如图乙所示.试求: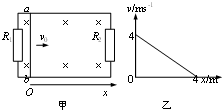 如图甲所示,质量为m=0.5kg、电阻r=1Ω的跨接杆ab可以无摩擦地沿水平固定导轨滑行,导轨足够长,两导轨间宽度为L=1m,导轨电阻不计,电阻R1=1.5Ω,R2=3Ω,装置处于竖直向下的匀强磁场中,磁感应强度为B=1T.杆从x轴原点O以水平初速度向右滑行,直到停止.已知杆在整个运动过程中v随位移x变化的关系如图乙所示.求:
如图甲所示,质量为m=0.5kg、电阻r=1Ω的跨接杆ab可以无摩擦地沿水平固定导轨滑行,导轨足够长,两导轨间宽度为L=1m,导轨电阻不计,电阻R1=1.5Ω,R2=3Ω,装置处于竖直向下的匀强磁场中,磁感应强度为B=1T.杆从x轴原点O以水平初速度向右滑行,直到停止.已知杆在整个运动过程中v随位移x变化的关系如图乙所示.求: