题目内容
7.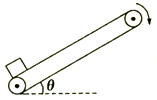 如图所示,足够长的传送带以恒定速率沿顺时针方向运转.现将一个物体轻轻放在传送带底端,物体第一阶段被加速到与传送带具有相同的速度,第二阶段匀速运动到传送带顶端.则下列说法中正确的是( )
如图所示,足够长的传送带以恒定速率沿顺时针方向运转.现将一个物体轻轻放在传送带底端,物体第一阶段被加速到与传送带具有相同的速度,第二阶段匀速运动到传送带顶端.则下列说法中正确的是( )| A. | 第一阶段和第二阶段摩擦力对物体都做正功 | |
| B. | 第一阶段摩擦力对物体做的功大于物体机械能的增加量 | |
| C. | 第二阶段摩擦力对物体做的功等于第二阶段物体机械能的增加量 | |
| D. | 第一阶段摩擦力与物体和传送带间的相对位移的乘积在数值上等于系统产生的内能 |
分析 功是能量转化的量度,合力做功是动能变化的量度;除重力外其余力做的功是机械能变化的量度;一对滑动摩擦力做的功是内能变化的量度;先对小滑块受力分析,再根据功能关系列式分析求解.
解答 解:A、对小滑块受力分析,受到重力、支持力和摩擦力,摩擦力一直沿斜面向上,故摩擦力一直做正功,故A正确;
B、第一阶段摩擦力对物体做的功,转化为物体的机械能,所以第一阶段摩擦力对物体做的功等于物体机械能的增加量.故B错误;
C、除重力外其余力做的功是机械能变化的量度,由于支持力不做功,故物体从底端到顶端全过程机械能的增加等于全过程摩擦力对物体所做的功,故C正确;
D、第一阶段摩擦力对物体所做的功一部分转化为物体的动能,另一部分转化为物体及传送带的内能;第二阶段,摩擦力对物体所做的功都转化为机械能,故摩擦力与相对位移的乘积在数值上等于系统产生的内能;故D正确;
故选:ACD.
点评 本题运用功能关系分析传送带问题,分析物体的运动情况和摩擦力的方向是解题的基础,根据动能定理和功能原理分析功能关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15. 如图所示,小球自a点由静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩到最短,若不计弹簧质量和空气阻力,在小球由a→b→c的运动过程中( )
如图所示,小球自a点由静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩到最短,若不计弹簧质量和空气阻力,在小球由a→b→c的运动过程中( )
 如图所示,小球自a点由静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩到最短,若不计弹簧质量和空气阻力,在小球由a→b→c的运动过程中( )
如图所示,小球自a点由静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩到最短,若不计弹簧质量和空气阻力,在小球由a→b→c的运动过程中( )| A. | 小球的加速度在ab段不变,在bc段逐渐减小 | |
| B. | 小球的重力势能减少 | |
| C. | 小球在b点时速度最大 | |
| D. | 小球的机械能守恒 |
12. 如图所示,质量为m的物体A静止于倾角为θ的斜面体B上,斜面体B的质量为M,现对该斜面体施加一个水平向左的推力F,使物体随斜面体一起沿水平方向向左匀速运动的位移为L,则在此运动过程中斜面体B对物体A所做的功为( )
如图所示,质量为m的物体A静止于倾角为θ的斜面体B上,斜面体B的质量为M,现对该斜面体施加一个水平向左的推力F,使物体随斜面体一起沿水平方向向左匀速运动的位移为L,则在此运动过程中斜面体B对物体A所做的功为( )
 如图所示,质量为m的物体A静止于倾角为θ的斜面体B上,斜面体B的质量为M,现对该斜面体施加一个水平向左的推力F,使物体随斜面体一起沿水平方向向左匀速运动的位移为L,则在此运动过程中斜面体B对物体A所做的功为( )
如图所示,质量为m的物体A静止于倾角为θ的斜面体B上,斜面体B的质量为M,现对该斜面体施加一个水平向左的推力F,使物体随斜面体一起沿水平方向向左匀速运动的位移为L,则在此运动过程中斜面体B对物体A所做的功为( )| A. | $\frac{fLm}{M+m}$ | B. | MgLcosθ | C. | 0 | D. | $\frac{1}{2}$mgLsin2θ |
19. 一自耦调压变压器(可看做理想变压器)的电路如图甲所示,移动滑动触头P可改变副线圈匝数.已知变压器线圈总匝数为1900匝;原线圈为1100匝,接在如图乙所示的交流电源上,电压表为理想电表.则( )
一自耦调压变压器(可看做理想变压器)的电路如图甲所示,移动滑动触头P可改变副线圈匝数.已知变压器线圈总匝数为1900匝;原线圈为1100匝,接在如图乙所示的交流电源上,电压表为理想电表.则( )
 一自耦调压变压器(可看做理想变压器)的电路如图甲所示,移动滑动触头P可改变副线圈匝数.已知变压器线圈总匝数为1900匝;原线圈为1100匝,接在如图乙所示的交流电源上,电压表为理想电表.则( )
一自耦调压变压器(可看做理想变压器)的电路如图甲所示,移动滑动触头P可改变副线圈匝数.已知变压器线圈总匝数为1900匝;原线圈为1100匝,接在如图乙所示的交流电源上,电压表为理想电表.则( )| A. | 交流电源电压瞬时值的表达式为u=220sin100πtV | |
| B. | P向上移动时,电压表的最大示数为380V | |
| C. | P向下移动时,原、副线圈的电流之比增大 | |
| D. | P向下移动时,变压器的输入功率变大 |
16.行星A绕太阳的运动视为匀速做圆周运动,其运行轨道半径为r,周期为T.观察发现,其实际运行的轨道与圆轨道存在一些偏离,且每隔时间t发生一次最大的偏离(计算时仍看成圆周运动).形成这种现象的原因可能是行星A外侧还存在着一颗未知行星B,它对行星A的万有引力引起A行星轨道的偏离,且行星A的轨道发生最大偏离时,A、B两行星相距最近.根据这些条件,可求得行星B的轨道半径为( )
| A. | ($\frac{t-T}{t}$)${\;}^{\frac{2}{3}}$r | B. | $\frac{t}{t-T}$r | C. | ($\frac{t}{t-T}$)${\;}^{\frac{2}{3}}$r | D. | ($\frac{t}{t+T}$)${\;}^{\frac{2}{3}}$r |
 在探究恒力做功与动能改变的关系实验中,已知砂和砂桶的质量为m,小车的质量为M,为了实验简便,须使小车受到的合外力可以看作砂和砂桶的总重力,回答下列问题:
在探究恒力做功与动能改变的关系实验中,已知砂和砂桶的质量为m,小车的质量为M,为了实验简便,须使小车受到的合外力可以看作砂和砂桶的总重力,回答下列问题: 甲、乙、丙三球的质量分别为2m,m,m排成的一直线放在光滑水平面上,如图所示,乙球与丙球靠在一起,且为静止,甲球以速度v向它们运动,若他们在对心碰撞中无机械能损失,求三球最终的速度?
甲、乙、丙三球的质量分别为2m,m,m排成的一直线放在光滑水平面上,如图所示,乙球与丙球靠在一起,且为静止,甲球以速度v向它们运动,若他们在对心碰撞中无机械能损失,求三球最终的速度?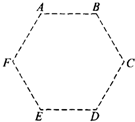 如图所示的A、B、C、D、E、F为匀强电场中正六边形的六个顶点.已知A、B、C三点的电势分别为-1V、1V、5V,则D点的电势为7V,E点的电势为5V.
如图所示的A、B、C、D、E、F为匀强电场中正六边形的六个顶点.已知A、B、C三点的电势分别为-1V、1V、5V,则D点的电势为7V,E点的电势为5V.