题目内容
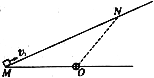
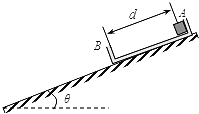
【题目】如图所示,在倾角30°的斜面上放置一个凹撸B,B与斜面间的动摩擦因数
；槽内靠近右侧壁处有一小物块A(可视为质点),它到凹槽左侧壁的距离
0.1m，A、B的质量都为m=2kg，B与斜面间的最大静摩擦力可认为等于滑动摩摞力,不计A、B之间的摩擦,斜面足够长。现同时由静止释放A、B,经过一段时间,A与B的侧壁发生碰撞,碰撞过程不计机械能损失,碰撞时间极短,g取
.求：
(1)释放后物块A和凹槽B的加速度分别是多大?
(2)物块A与凹槽B的左侧壁第一次碰撞后瞬间A、B的速度大小；
(3)从初始位置到物块A与凹糟B的左侧壁发生第三次碰撞时B的位移大小。
【答案】（1）（2）vAn=(n-1)ms-1，vBn="n" ms-1（3）xn总=0.2n2m
【解析】
（1）设物块A的加速度为a1，则有mAgsinθ=ma1，
解得a1=5m/s2
凹槽B运动时受到的摩擦力f=μ×3mgcosθ=mg方向沿斜面向上；
凹槽B所受重力沿斜面的分力G1=2mgsinθ=mg方向沿斜面向下；
因为G1=f，则凹槽B受力平衡，保持静止，凹槽B的加速度为a2=0
（2）设A与B的左壁第一次碰撞前的速度为vA0，根据运动公式：v2A0=2a1d
解得vA0=3m/s；
AB发生弹性碰撞，设A与B第一次碰撞后瞬间A的速度大小为vA1，B的速度为vB1，则由动量守恒定律：
；
由能量关系：
解得vA1=-1m/s(负号表示方向)，vB1=2m/s
练习册系列答案
金钥匙试卷系列答案
相关题目
