题目内容
7. 如图所示,AB为光滑半圆轨道ACB的水平直径,C为环上的最低点,环半径为R,设重力加速度为g,不计空气阻力.
如图所示,AB为光滑半圆轨道ACB的水平直径,C为环上的最低点,环半径为R,设重力加速度为g,不计空气阻力.(1)若将一质量为m的小球从A点由静止释放,求运动到C点的速度大小及对C点的压力大小?
(2)若将该小球从A点以速度v0被水平抛出,要使小球落到环上时的竖直分速度最大,v0为多大?
分析 (1)根据动能定理求出小球运动到C点的速度大小,根据牛顿第二定律求出C点的支持力,从而得出压力的大小.
(2)下降的高度越大,竖直分速度越大,根据运动学公式,结合等时性求出初速度的大小.
解答 解:(1)从A到C,根据动能定理得,mgR=$\frac{1}{2}$mv2
解得v=$\sqrt{2gR}$
FN-mg=$m\frac{{v}^{2}}{R}$
解得 FN=3mg
根据牛顿第三定律知,小球对C点的压力为3mg.
(2)小球落到C点时竖直分速度最大,则R=v0t
R=$\frac{1}{2}$gt2
解得v0=$\sqrt{\frac{gR}{2}}$.
答:(1)运动到C点的速度大小为$\sqrt{2gR}$,对C点的压力为3mg.
(2)v0的大小为$\sqrt{\frac{gR}{2}}$.
点评 本题考查了平抛运动和圆周运动的基本运用,知道圆周运动向心力的来源和平抛运动在水平方向和竖直方向上的运动规律是解决本题的关键.

练习册系列答案
相关题目
17.甲、乙、丙三个物体运动的 x-t图象如图所示,下列说法中正确的是( )


| A. | 丙物体做加速直线运动 | |
| B. | 甲物体做曲线运动 | |
| C. | 三个物体在0-t0时间内平均速度$\overline{{v}_{甲}}$>$\overline{{v}_{丙}}$>$\overline{{v}_{乙}}$ | |
| D. | 三个物体在0-t0时间内平均速率$\overline{{v}_{甲}}$>$\overline{{v}_{丙}}$>$\overline{{v}_{乙}}$ |
18.篮球运动员通常要伸出两臂迎接传来的篮球.接球时,两臂随球迅速收缩至胸前.这样做可以( )
| A. | 减小球对手的冲量 | B. | 减小球的动量变化量 | ||
| C. | 减小球对人的冲击力 | D. | 减小球的能量变化量 |
15.质量为60kg的建筑工人,不慎从高空跌下,幸好弹性安全带的保护,使他悬挂起来.已知弹性安全带的缓冲时间是1.5s,安全带自然长度为5m,g取10m/s2,则弹性安全带所受的平均冲力的大小为( )
| A. | 500N | B. | 1100N | C. | 600N | D. | 1000N |
12.对平抛运动的说法正确的是( )
| A. | 初速度沿水平方向,不受重力作用 | |
| B. | 初速度沿水平方向,且只受重力作用 | |
| C. | 水平分运动与竖直分运动的时间不相等 | |
| D. | 以上情况都可能 |
19. 如图,质量相同的两物体a、b,用不可伸长的轻绳跨接在同一光滑的轻质定滑轮两侧,a在水平桌面的上方,b在水平粗糙桌面上.初始时用力压住b使a、b静止,撤去此压力后,a开始运动,在a下降的过程中,b始终未离开桌面.在此过程中( )
如图,质量相同的两物体a、b,用不可伸长的轻绳跨接在同一光滑的轻质定滑轮两侧,a在水平桌面的上方,b在水平粗糙桌面上.初始时用力压住b使a、b静止,撤去此压力后,a开始运动,在a下降的过程中,b始终未离开桌面.在此过程中( )
 如图,质量相同的两物体a、b,用不可伸长的轻绳跨接在同一光滑的轻质定滑轮两侧,a在水平桌面的上方,b在水平粗糙桌面上.初始时用力压住b使a、b静止,撤去此压力后,a开始运动,在a下降的过程中,b始终未离开桌面.在此过程中( )
如图,质量相同的两物体a、b,用不可伸长的轻绳跨接在同一光滑的轻质定滑轮两侧,a在水平桌面的上方,b在水平粗糙桌面上.初始时用力压住b使a、b静止,撤去此压力后,a开始运动,在a下降的过程中,b始终未离开桌面.在此过程中( )| A. | a的动能大于b的动能 | |
| B. | 两物体机械能的变化量相等 | |
| C. | a的重力势能的减小量等于两物体总动能的增加量 | |
| D. | 绳的拉力对a所做的功与对b所做的功的代数和为零 |
16. 如图所示,将一劲度系数为k的轻弹簧一端固定在内壁光滑的半球形容器水平直径A处,O为球心,弹簧另一端与质量为m的小球相连,小球静止于P点.已知容器半径为R、与水平地面之间的动摩擦因数为μ,OP与水平直径的夹角为θ=60°,下列说法正确的是( )
如图所示,将一劲度系数为k的轻弹簧一端固定在内壁光滑的半球形容器水平直径A处,O为球心,弹簧另一端与质量为m的小球相连,小球静止于P点.已知容器半径为R、与水平地面之间的动摩擦因数为μ,OP与水平直径的夹角为θ=60°,下列说法正确的是( )
 如图所示,将一劲度系数为k的轻弹簧一端固定在内壁光滑的半球形容器水平直径A处,O为球心,弹簧另一端与质量为m的小球相连,小球静止于P点.已知容器半径为R、与水平地面之间的动摩擦因数为μ,OP与水平直径的夹角为θ=60°,下列说法正确的是( )
如图所示,将一劲度系数为k的轻弹簧一端固定在内壁光滑的半球形容器水平直径A处,O为球心,弹簧另一端与质量为m的小球相连,小球静止于P点.已知容器半径为R、与水平地面之间的动摩擦因数为μ,OP与水平直径的夹角为θ=60°,下列说法正确的是( )| A. | 容器与水平地面间的摩擦力方向向左 | |
| B. | 容器与水平地面间的摩擦力方向向右 | |
| C. | 弹簧原长为R-$\frac{mg}{\sqrt{3}k}$ | |
| D. | 剪断弹簧的瞬间,小球的加速度和速度均为零 |
17.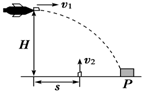 如图所示,在一次空地演习中,离地H高处的飞机发射一颗炸弹,炸弹以水平速度v1出欲轰炸地面目标P,反应灵敏的地面拦截系统同时以速度v2直向上发射炮弹进行拦截.设飞机发射炸弹时与拦截系统的水平距离为s,若拦截成功,不计空气阻力,则v1,v2系满足( )
如图所示,在一次空地演习中,离地H高处的飞机发射一颗炸弹,炸弹以水平速度v1出欲轰炸地面目标P,反应灵敏的地面拦截系统同时以速度v2直向上发射炮弹进行拦截.设飞机发射炸弹时与拦截系统的水平距离为s,若拦截成功,不计空气阻力,则v1,v2系满足( )
 如图所示,在一次空地演习中,离地H高处的飞机发射一颗炸弹,炸弹以水平速度v1出欲轰炸地面目标P,反应灵敏的地面拦截系统同时以速度v2直向上发射炮弹进行拦截.设飞机发射炸弹时与拦截系统的水平距离为s,若拦截成功,不计空气阻力,则v1,v2系满足( )
如图所示,在一次空地演习中,离地H高处的飞机发射一颗炸弹,炸弹以水平速度v1出欲轰炸地面目标P,反应灵敏的地面拦截系统同时以速度v2直向上发射炮弹进行拦截.设飞机发射炸弹时与拦截系统的水平距离为s,若拦截成功,不计空气阻力,则v1,v2系满足( )| A. | v1=v2 | B. | v1=$\frac{S}{H}$v2 | C. | v1=$\sqrt{\frac{H}{S}}$v2 | D. | v1=$\sqrt{\frac{S}{H}}$v2 |
 如图所示,光滑水平轨道与光滑圆弧轨道相切,轻弹簧的一端固定在轨道的左端,OP是可绕O转动的轻杆,且摆到某处即能停在该处;另有一小钢球.现要利用这些器材测定弹簧被压缩一定量时的弹性势能:( 重力加速度为g )
如图所示,光滑水平轨道与光滑圆弧轨道相切,轻弹簧的一端固定在轨道的左端,OP是可绕O转动的轻杆,且摆到某处即能停在该处;另有一小钢球.现要利用这些器材测定弹簧被压缩一定量时的弹性势能:( 重力加速度为g )