��Ŀ����
����Ŀ����ͼ��ʾ����ֱ������һ���̶�Բ����MN��������ֱ�����ϵ�ֱ���������⻬����MP��QN�Ķ˵㶼��Բ���ϣ�MP��QN����������ȫ��ͬ��С��a��b�ֱ��M��Q�������ͷţ������Ǹ�����MP��QN�˶���Բ���ϵĹ����У�����˵������ȷ���ǣ�������
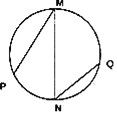
A. ����Ķ����仯��С��ͬ B. ����������ij�����С��ͬ
C. ������a��ij����ϴ� D. ������a��ij����ϴ�
���𰸡�BC
���������⣺��С����������֧�������������ع���ķ���ʹ�ֱ�˵ķ��������ֽ⣬����ţ�ٵڶ����ɵ�С����������Ϊ����ȼ���ֱ���˶��ļ��ٶ�Ϊ
a=gsin�ȣ���Ϊ����ˮƽ����ļнǣ�
��ͼ�е�ֱ�������ο�֪��С������λ��S=2Rsin��
����![]() ��t����أ���t1=t2
��t����أ���t1=t2
A��C��С���ܵ��ĺ��������������ع������ķ���������mgsin�ȣ����Ժ������ij�����СΪ��mgsin��t����ͼ��֪MP��ˮƽ����֮��ļнǴ�������MP�˶���a���ܵ��ĺ������ij�������MP�˶���a���ܵ��ĺ������ij������ɶ���������֪��a��Ķ����仯��A����C��ȷ��
B�������ij���Ϊmgt�������˶���ʱ����ȣ����������ij�����С��ȣ���B��ȷ��
D�������ij�����mgcos��t����ͼ��֪MP��ˮƽ����֮��ļнǴ�����a��ĵ����ij���С����D����
��ѡ��BC