题目内容
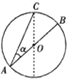
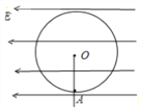
【题目】如图所示，水平向左的匀强电场中，用长为l的绝缘轻质细绳悬挂一小球，小球质量为m，带电量为+q，将小球拉至竖直位置最低位置A点处无初速释放，小球将向左摆动，细线向左偏离竖直方向的最大角度θ=74°。
(1)求电场强度的大小E；
(2)将小球向左摆动的过程中，对细线拉力的最大值；
(3)若从A点处释放小球时，给小球一个水平向左的初速度
，则为保证小球在运动过程中细线不会松弛， 
的大小应满足什么条件?
【答案】（1）
；（2）
；（3）
【解析】(1)由于带电小球所受电场力方向向左，电场线方向也向左，细线向左偏离竖直方向的最大角度θ=74°，根据动能定理：
解得：E=
；
(2)小球运动的过程中速度最大的位置，由动能定理得：
小球在370时，由重力电场力与细线的拉力的合力提供向心力，根据牛顿第二定律得：
FTmgsin37°qEcos37°=mv2/L
解得：FT=7mg/4
（3）为保证细线不会松弛，小球在与竖直方向的夹角37°的右上方应满足：
根据动能定理： 
，
联立解得： 
；
练习册系列答案
相关题目
