题目内容
8. 如图所示,在桌面上方有一倒立的玻璃圆锥,顶角∠AOB=120°,顶点O与桌面的距离为4a,圆锥的底面半径R=a,圆锥轴线与桌面垂直.有一半径为R的圆柱形平行光束垂直入射到圆锥的底面上,光束的中心轴与圆锥的轴重合.已知玻璃的折射率n=$\sqrt{3}$,求光束在桌面上形成的光斑的面积.
如图所示,在桌面上方有一倒立的玻璃圆锥,顶角∠AOB=120°,顶点O与桌面的距离为4a,圆锥的底面半径R=a,圆锥轴线与桌面垂直.有一半径为R的圆柱形平行光束垂直入射到圆锥的底面上,光束的中心轴与圆锥的轴重合.已知玻璃的折射率n=$\sqrt{3}$,求光束在桌面上形成的光斑的面积.
分析 当半径为R的圆柱形平行光束垂直入射到圆锥的底面上,经过第一次折射时,由于入射角等于零,所以折射角也是零,因此折射光线不发生偏折.当第二次折射时,由于入射角等于30°,而玻璃的折射率n=$\sqrt{3}$,可得临界角与入射角的关系,判断光线不会发生光的全反射,作出光路图,可根据几何关系可确定光斑的半径,即可求得光斑的面积.
解答  解:设玻璃的临界角为C,则有:sinC=$\frac{1}{n}$=$\frac{1}{\sqrt{3}}$
解:设玻璃的临界角为C,则有:sinC=$\frac{1}{n}$=$\frac{1}{\sqrt{3}}$
如图所示,射到OA界面的入射角为:α=30°,
则有:sinα=$\frac{1}{2}$<sinC,α<C
故入射光线能从圆锥侧面射出.
设折射角为β,无限接近A点的折射光线为AC,根据折射定律有:
sinβ=nsinα
解得:β=60°
过O点作OD∥AC,则∠O2OD=β-α=30°
在直角三角形O1AO中,O1O=Rtan30°=$\frac{\sqrt{3}}{3}$a
在直角三角形△ACE中,EC=AEtan30°=(4a+$\frac{\sqrt{3}}{3}$a)$•\frac{\sqrt{3}}{3}$=$\frac{4\sqrt{3}+1}{3}$a
故O2C=EC-R=$\frac{4\sqrt{3}-2}{3}$a
O2D=O2Otan30°=4atan30°=$\frac{4\sqrt{3}}{3}$a
光束在桌面上形成光环的面积
S=π•O2D2-π•O2C2=$\frac{16\sqrt{3}-4}{9}$πa2
答:光束在桌面上形成的光照亮部分的面积为$\frac{16\sqrt{3}-4}{9}$πa2.
点评 本题关键之处是根据光的折射定律与反射定律作出光路图,再利用几何关系来辅助计算.

练习册系列答案
相关题目
19.下列说法正确的是( )
| A. | 一条沿自身长度方向运动的杆,其长度总比杆静止时长 | |
| B. | 根据多普勒效应可以判断遥远天体相对于地球的运动速度 | |
| C. | 大量事实证明,电磁波不能产生衍射现象 | |
| D. | 受迫振动的频率总等于系统的固有频率 |
3. 如图所示,理想变压器原线圈输入电压u=Umsinωt,副线圈电路中R0为定值电阻,R是滑动变阻器.V1和V2是理想交流电压表,示数分别用U1和U2表示;A1和A2是理想交流电流表,示数分别用I1和I2表示.下列说法正确的是( )
如图所示,理想变压器原线圈输入电压u=Umsinωt,副线圈电路中R0为定值电阻,R是滑动变阻器.V1和V2是理想交流电压表,示数分别用U1和U2表示;A1和A2是理想交流电流表,示数分别用I1和I2表示.下列说法正确的是( )
 如图所示,理想变压器原线圈输入电压u=Umsinωt,副线圈电路中R0为定值电阻,R是滑动变阻器.V1和V2是理想交流电压表,示数分别用U1和U2表示;A1和A2是理想交流电流表,示数分别用I1和I2表示.下列说法正确的是( )
如图所示,理想变压器原线圈输入电压u=Umsinωt,副线圈电路中R0为定值电阻,R是滑动变阻器.V1和V2是理想交流电压表,示数分别用U1和U2表示;A1和A2是理想交流电流表,示数分别用I1和I2表示.下列说法正确的是( )| A. | I1、I2表示电流的有效值,U1、U2表示电压的瞬时值 | |
| B. | 变压器的输入功率I1U1 与输出功率I2U2 相等 | |
| C. | 滑动触头P向下滑动,U2变小、I2变小 | |
| D. | 滑动触头P向下滑动过程中,U1变大、I1变大 |
13. 滑雪运动员沿倾角一定的斜坡向下滑行时其速度-时间图象如图所示,图线为曲线.则此过程中运动员的( )
滑雪运动员沿倾角一定的斜坡向下滑行时其速度-时间图象如图所示,图线为曲线.则此过程中运动员的( )
 滑雪运动员沿倾角一定的斜坡向下滑行时其速度-时间图象如图所示,图线为曲线.则此过程中运动员的( )
滑雪运动员沿倾角一定的斜坡向下滑行时其速度-时间图象如图所示,图线为曲线.则此过程中运动员的( )| A. | 速度越来越大 | B. | 加速度越来越小 | C. | 阻力越来越小 | D. | 机械能保持不变 |
1.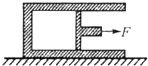 如图所示,绝热气缸固定在水平地面上,气缸内用绝热活塞封闭着一定质量的理想气体.开始时活塞静止在图示位置,现用力F使活塞缓慢向右移动一段距离,则在此过程中( )
如图所示,绝热气缸固定在水平地面上,气缸内用绝热活塞封闭着一定质量的理想气体.开始时活塞静止在图示位置,现用力F使活塞缓慢向右移动一段距离,则在此过程中( )
 如图所示,绝热气缸固定在水平地面上,气缸内用绝热活塞封闭着一定质量的理想气体.开始时活塞静止在图示位置,现用力F使活塞缓慢向右移动一段距离,则在此过程中( )
如图所示,绝热气缸固定在水平地面上,气缸内用绝热活塞封闭着一定质量的理想气体.开始时活塞静止在图示位置,现用力F使活塞缓慢向右移动一段距离,则在此过程中( )| A. | 缸内气体对活塞做负功 | |
| B. | 缸内气体的内能减小 | |
| C. | 缸内气体在单位时间内作用于活塞单位面积的冲量增大 | |
| D. | 缸内气体分子在单位时间内与活塞碰撞的次数增加 |

 如图所示,一艘赛艇停在平静的水面上,赛艇前部上端有一标记P,在其正前方A处有一浮标.潜水员从P前方S=4m处开始下潜,当下潜至深度为H=2$\sqrt{7}$m的B处时,才能看到赛艇尾端后方水面上的景物,且看到P刚好被浮标挡住.测得PA、BA与竖直方向的夹角分别为53°和37°.忽略赛艇吃水深度,求赛艇的长度L.sin53°=0.8,cos53°=0.6.
如图所示,一艘赛艇停在平静的水面上,赛艇前部上端有一标记P,在其正前方A处有一浮标.潜水员从P前方S=4m处开始下潜,当下潜至深度为H=2$\sqrt{7}$m的B处时,才能看到赛艇尾端后方水面上的景物,且看到P刚好被浮标挡住.测得PA、BA与竖直方向的夹角分别为53°和37°.忽略赛艇吃水深度,求赛艇的长度L.sin53°=0.8,cos53°=0.6. 如图,纸面内直线MN左侧边长为L的正方形区域OACD中.有方向平行于AC的匀强电场.O处的粒子源沿垂直于AC方向发射速度为v0的正电粒子,粒子质量为m、电荷量为q.粒子恰好从AC的中点P经过.不计粒子重力.
如图,纸面内直线MN左侧边长为L的正方形区域OACD中.有方向平行于AC的匀强电场.O处的粒子源沿垂直于AC方向发射速度为v0的正电粒子,粒子质量为m、电荷量为q.粒子恰好从AC的中点P经过.不计粒子重力.  如图所示,水平轨道与半径为R的光滑半圆轨道相切,半圆轨道的左道的左侧存在着场强E=50N/C方向竖直向上的匀强电场和次感应强度B=1.25T垂直纸面向里的匀强磁场,在水平轨道上一个质量为m=0.01kg、电荷量为q=+10-3C的带电小球A以初速度为V0=40m/s向右运动,小球A与水平轨道间的动摩擦因数为0.5,在光滑半圆轨道最低点停放一个质量为M=0.3kg的不带电绝缘小球B,两个小球均可看成质点,小球A与小球B碰撞后以V1=20m/s的速度向左运动,小球B沿圆轨道运动到最高点水平抛出,g=10m/s2.求当圆轨道半径R取值多大值时,B球的平抛水平距离最大?最大值是多少?
如图所示,水平轨道与半径为R的光滑半圆轨道相切,半圆轨道的左道的左侧存在着场强E=50N/C方向竖直向上的匀强电场和次感应强度B=1.25T垂直纸面向里的匀强磁场,在水平轨道上一个质量为m=0.01kg、电荷量为q=+10-3C的带电小球A以初速度为V0=40m/s向右运动,小球A与水平轨道间的动摩擦因数为0.5,在光滑半圆轨道最低点停放一个质量为M=0.3kg的不带电绝缘小球B,两个小球均可看成质点,小球A与小球B碰撞后以V1=20m/s的速度向左运动,小球B沿圆轨道运动到最高点水平抛出,g=10m/s2.求当圆轨道半径R取值多大值时,B球的平抛水平距离最大?最大值是多少?