题目内容
18.《愤怒的小鸟》是一款非常流行的游戏,故事也相当有趣,如图甲,为了报复偷走鸟蛋的肥猪们,鸟儿以自己的身体为武器,如炮弹般弹射出去攻击肥猪们的堡垒.假设小鸟被弹弓沿水平方向弹出,如图乙所示.(取重力加速度g=10m/s2)
(1)若h1=3.6m,l1=2.4m,h2=1.8m,要使小鸟飞出去能直接打中肥猪的堡垒,小鸟的初速度v0应多大?
(2)如果小鸟弹出后,先掉到平台上(此时小鸟距抛出点的水平距离为l2),接触平台瞬间竖直速度变为零,水平速度不变,小鸟在平台上滑行一段距离后,若要打中肥猪的堡垒,小鸟和平台间的动摩擦因数μ应满足什么关系(用题中所给的符号h1,l1,h2,l2,g表示)?
分析 (1)设小鸟以v0弹出能直接击中堡垒,由平抛运动的基本公式列式即可求解;
(2)对小鸟在平台上滑行初速度仍为v0,若刚好击中堡垒,则有末速度为v=0,由动能定律列式即可求解.
解答 解:(1)设小鸟以v0弹出能直接击中堡垒,则由平抛运动规律,有:
h1-h2=$\frac{1}{2}g{t}^{2}$,
l1=v0t
联立解得:t=0.6 s,v0=4m/s.
(2)对小鸟在平台上滑行初速度仍为v0,若刚好击中堡垒,则有末速度为:v=0
由动能定理有:-μmg(l1-l2)=$\frac{1}{2}m{v}^{2}-\frac{1}{2}m{{v}_{0}}^{2}$,
解得:μ=$\frac{{{v}_{0}}^{2}}{2g({l}_{1}-{l}_{2})}$.
可见,μ与v0应满足$μ≤\frac{{{v}_{0}}^{2}}{2g({l}_{1}-{l}_{2})}$才能打中堡垒.
答:(1)小鸟飞出去的初速度应为4m/s;
(2)μ与v0应满足$μ≤\frac{{{v}_{0}}^{2}}{2g({l}_{1}-{l}_{2})}$.
点评 解决本题的关键知道平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动.难度适中.

练习册系列答案
相关题目
9.下列说法中不正确的是( )
| A. | 电动机是把其他形式的能转化为电能的装置 | |
| B. | 发电机是把其他形式的能转化为电能的装置 | |
| C. | 电容器是储存电荷的装置 | |
| D. | 白炽灯是利用电流的热效应工作的 |
6.崔牛先生向客户推介他设计的“超级推进器”,该推进器由超导体、激光器、致冷剂以及计算机控制系统组成,其神奇之处在于能通过自身的循环工作,源源不断地获得动力,而不需要消耗任何能源.事实上,这是不可能实现的,因为他的设计违反了( )
| A. | 能量守恒定律 | B. | 电荷守恒定律 | C. | 机械能守恒定律 | D. | 质量守恒定律 |
13.现代社会越来越智能化,而智能化就离不开传感器,请问下列常见物品中使用了温度传感器的是( )
| A. | 电冰箱 | B. | 遥控器 | C. | 教室走廊灯 | D. | 宾馆火灾报警器 |
3.在电梯匀速上升的过程中,站在电梯里的人( )
| A. | 所受支持力做负功,机械能减少 | B. | 所受支持力做负功,机械能增加 | ||
| C. | 所受支持力做正功,机械能减少 | D. | 所受支持力做正功,机械能增加 |
10.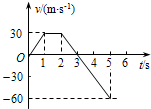 某军事试飞场正在地面上试航一种新型飞行器,若某次试飞中,飞行器在竖直方向飞行的v-t图象如图所示,则下列说法中正确的是( )
某军事试飞场正在地面上试航一种新型飞行器,若某次试飞中,飞行器在竖直方向飞行的v-t图象如图所示,则下列说法中正确的是( )
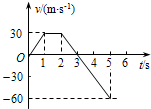 某军事试飞场正在地面上试航一种新型飞行器,若某次试飞中,飞行器在竖直方向飞行的v-t图象如图所示,则下列说法中正确的是( )
某军事试飞场正在地面上试航一种新型飞行器,若某次试飞中,飞行器在竖直方向飞行的v-t图象如图所示,则下列说法中正确的是( )| A. | 0~1s内飞行器匀速上升 | B. | 1s~2s内飞行器静止不动 | ||
| C. | 3s末飞行器回到地面 | D. | 5s末飞行器恰好回到地面 |

 如图所示,在桌面上方有一倒立的玻璃圆锥,顶角∠AOB=120°,顶点O与桌面的距离为4a,圆锥的底面半径R=a,圆锥轴线与桌面垂直.有一半径为R的圆柱形平行光束垂直入射到圆锥的底面上,光束的中心轴与圆锥的轴重合.已知玻璃的折射率n=$\sqrt{3}$,求光束在桌面上形成的光斑的面积.
如图所示,在桌面上方有一倒立的玻璃圆锥,顶角∠AOB=120°,顶点O与桌面的距离为4a,圆锥的底面半径R=a,圆锥轴线与桌面垂直.有一半径为R的圆柱形平行光束垂直入射到圆锥的底面上,光束的中心轴与圆锥的轴重合.已知玻璃的折射率n=$\sqrt{3}$,求光束在桌面上形成的光斑的面积.