题目内容
(17分）如图，一轨道由光滑竖直的1/4圆弧AB,粗糙水平面BC及光滑斜面CE组成，BC与CE在C点由极小光滑圆弧相切连接，斜面与水平面的夹角θ=30°，一小物块从A点正上方高h=0.2 m处P点自由下落，正好沿A点切线进入轨道，已知小物块质量m=1kg,圆弧半径R=0.05 m, BC长s=0.1m,小物块过C点后经过时间t1=0.3s第一次到达图中的D点，又经t2=0.2s第二次到达刀点。取g=10m/ s2.求：
（1）小物块第一次到达圆弧轨道B点的瞬间，受到轨道弹力N的大小？
（2）小物块与水平面BC间的动摩擦因数
=？
（3）小物块最终停止的位置？
（1）110N（2）
（3）球最终停在C点
【解析】
试题分析：(1) 设小球在B点时速度大小为vB，从A点到B点的过程由动能定理得
在圆弧轨道B点即圆周最低点，有
解得
(2) 设小球在CE段加速度为a，则沿斜面方向受力分析可得
设小球第一次经过C点的速度为
，从C点上滑到最高点，设经过的时间是t，则
从C点到最高点，匀减速
小球从B到C，根据动能定理
得
(3) 设小球在B点动能为EB，每次经过BC段损失的能量为△E，则
=2.5J
其他各段无能量损失,可得
，所以小球最终停在C点。
考点：动能定理 匀变速直线运动
暑假作业安徽少年儿童出版社系列答案
神舟十号在酒泉卫星发射中心“921工位”，2013年6月11日17时38分，由长征二号F改进型运载火箭（遥十）“神箭”成功发射．在轨飞行十五天左右，加上发射与返回，其中停留天宫一号十二天，6月13日与天宫一号进行对接．．假如神舟十号与天宫一号对接前所处的轨道如图所示，当它们处于如图所示的轨道运行时，下列说法正确的是（ ）
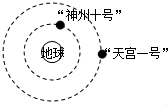2013年6月11日17时38分“神舟十号”飞船搭载三位航天员飞向太空，“神舟十号”是中国“神舟”号系列飞船之一，它是中国第五艘搭载太空人的飞船．飞船由推进舱、返回舱、轨道舱和附加段组成．升空后再和目标飞行器“天宫一号”对接，并对其进行短暂的有人照管试验．飞船将在轨飞行15天，并首次开展我国航天员太空授课活动．如图所示，“神舟十号”和“天宫一号”均绕地球做匀速圆周运动，则“神州十号”载人飞船与“天宫一号”飞船相比（ ）| A、“神州十号”运行速度较大 | B、“神州十号”运行角速度较大 | C、“神州十号”运行周期较大 | D、“神州十号”运行的向心加速度较大 |
2013年6月11日17时38分“神舟十号”飞船搭载三位航天员飞向太空，“神舟十号”是中国“神舟”号系列飞船之一，它是中国第五艘搭载太空人的飞船。飞船由推进舱、返回舱、轨道舱和附加段组成。升空后再和目标飞行器“天宫一号”对接，并对其进行短暂的有人照管试验。飞船将在轨飞行15天，并首次开展我国航天员太空授课活动。如图所示，“神舟十号”和“天宫一号”均绕地球做匀速圆周运动，则“神州十号”载人飞船与“天宫一号”飞船相比：
| A．“神州十号”运行速度较大 |
| B．“神州十号”运行角速度较大 |
| C．“神州十号”运行周期较大 |
| D．“神州十号”运行的向心加速度较大 |
如图17（甲）所示，弯曲部