题目内容
(14分)处于匀强磁场中的两根足够长、电阻不计的平行光滑金属导轨相距1m,导轨平面与水平面成θ=37°角,下端连接电阻或电容器.匀强磁场方向与导轨平面垂直,磁感应强度的大小B=2T,质量为0.02 kg、电阻不计的金属棒放在两导轨上,棒与导轨垂直并保持良好接触。若将下端连接阻值为R=20Ω的电阻,如图所示,(g取10 m/s2,sin 37°=0.6,cos 37°=0.8)

(1) 当金属棒下滑速度达到稳定时,求该速度的大小.
(2) 当金属棒下滑速度达到0.4m/s时,求加速度的大小.
(3) 若将下端连接的电阻换成电容为C=10000μF的电容器,求金属棒下滑的加速度.

(1) 当金属棒下滑速度达到稳定时,求该速度的大小.
(2) 当金属棒下滑速度达到0.4m/s时,求加速度的大小.
(3) 若将下端连接的电阻换成电容为C=10000μF的电容器,求金属棒下滑的加速度.
(1)0.6m/s(2)a1=2m/s2(3)a1=2m/s2
试题分析:(1)当金属棒速度稳定时,金属棒匀速运动,
当金属棒速度稳定时:

由法拉第电磁感应定律和闭合电路欧姆定律
 ,
,
解得:

(2)当速度v1=0.4m/s时:由法拉第电磁感应定律和闭合电路欧姆定律
 ,
,
由牛顿第二定律知:

解得:a1=2m/s2
(3)换成电容器时t时刻棒的速度为v,则棒产生的电动势和电容器充电电量
 ,
,
解得:
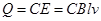
在
 时间内电荷量变化为
时间内电荷量变化为
故
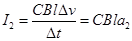
则牛顿第二定律知
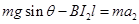
即

解得:
 m/s2
m/s2
练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目

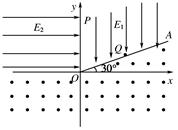


 向右运动。如果加一个竖直向下的匀强磁场,经过一段时间后,该质点的速度第一次变为与初始时刻的速度大小相等、方向相反;如果不加匀强磁场而改为加一个沿水平方向的匀强电场,经过相同的一段时间后,该质点的速度也第一次变为与初始时刻的速度大小相等、方向相反,则所加的匀强磁场的磁感应强度
向右运动。如果加一个竖直向下的匀强磁场,经过一段时间后,该质点的速度第一次变为与初始时刻的速度大小相等、方向相反;如果不加匀强磁场而改为加一个沿水平方向的匀强电场,经过相同的一段时间后,该质点的速度也第一次变为与初始时刻的速度大小相等、方向相反,则所加的匀强磁场的磁感应强度 和所加的匀强电场的电场强度
和所加的匀强电场的电场强度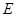 的比值
的比值 为
为


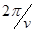


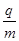 ;
;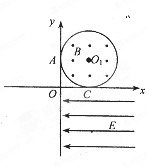
 ,忽略粒子的重力。求:
,忽略粒子的重力。求:
 ;
;