题目内容
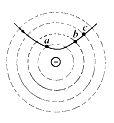
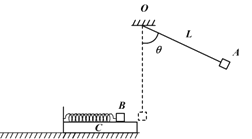
【题目】如图所示,物块C质量mc=4kg,上表面光滑,左边有一立柱,放在光滑水平地面上.一轻弹簧左端与立柱连接,右端与物块B连接,mB=2kg.长为L=3.6m的轻绳上端系于O点,下端系一物块A,mA=3kg.拉紧轻绳使绳与竖直方向成60°角,将物块A从静止开始释放,达到最低点时炸裂成质量m1=2kg、m2=1kg的两个物块1和2,物块1水平向左运动与B粘合在一起,物块2仍系在绳上具有水平向右的速度,刚好回到释放的初始点.A、B都可以看成质点.取g=10m/s2.求:
(1)设物块A在最低点时的速度v0和轻绳中的拉力F大小.
(2)物块A炸裂时增加的机械能△E.
(3)在以后的过程中,弹簧最大的弹性势能Epm.
【答案】(1)60N
(2)108J
(3)36J
【解析】试题分析:(1)物块A炸裂前的速度为v0,由动能定理有
mAgL(1﹣cos60°)=![]() mAv02①
mAv02①
解得 v0=6m/s
在最低点,根据牛顿第二定律有
F﹣mAg=mA![]() ②
②
由①②式解得 F=mAg+2mAg (1﹣cos60°)=60N
(2)设物块1的初速度为v1,物块2的初速度为v2,则v2=v0
由动量守恒定律得mAv0=m1v1﹣m2v2
解得v1=12m/s
△E=![]() m1v12+
m1v12+![]() m2v22﹣
m2v22﹣![]() mAv02
mAv02
解得△E="108" J
(3)设物块1 与B粘合在一起的共同速度为vB,由动量守恒
m1v1=(m1+mB)vB
所以vB="6" m/s
在以后的过程中,当物块C和1、B的速度相等时,弹簧的弹性势能最大,设共同速度为vm,由动量守恒
(m1+mB)vB=(m1+mB+mC)vm
有vm="3" m/s
由能量守恒得
Epm=![]() (m1+m2)vB2﹣
(m1+m2)vB2﹣![]() m1+mB+mC)vm2
m1+mB+mC)vm2
得Epm="36" J

练习册系列答案
相关题目