��Ŀ����
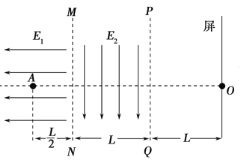
����Ŀ����ͼ��ʾ������MN�����һ��ǿΪE1��E����ǿ�糡��������ƽ�е�����MN��PQ֮������ſ�ΪL���糡ǿ��ΪE2��2E����ǿ�糡��������PQ�Ҳ����ΪL����һ��糡E2ƽ�е������ֽ�һ���ӣ������Ϊe������Ϊm�����ٶȵط���糡E1�е�A�㣬�����Ӵ����Ҳ�����ϣ�AO����������ֱ������ΪO�������������Բ��ơ���
��1�����Ӵ��ͷŵ����������õ�ʱ�䣻
��2�����Ӹ�����糡E2ʱ���ٶȷ�����AO���нǦȵ�����ֵtan �ȣ�
��3�����Ӵ����ϵĵ�P�䵽��O�ľ���y��
���𰸡���1��![]() ��2��2��3��3L
��2��2��3��3L
��������
�����������1�������ڵ糡E1�������ٶ�Ϊ����ȼ���ֱ���˶�������ٶ�Ϊa1��ʱ��Ϊt1����ţ�ٵڶ����ɺ��˶�ѧ��ʽ�ã� ![]()
![]()
v1��a1t1
![]()
�˶�����ʱ��Ϊt��t1��t2��![]()
��2�����������糡E2ʱ��ƽ�е糡�߷�����ٶ�Ϊvy������ţ�ٵڶ����ɵã������ڵ糡�еļ��ٶ�Ϊ
![]()
![]()
vy��a2t3
![]()
�����tan ����2
��3����ͼ��������ڵ糡�е�ƫת����Ϊy1���뿪�糡����ƽ�е糡����ƫ�ƾ���Ϊy2 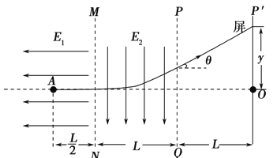
y1��![]() a2t
a2t
![]()
���x��y1��y2��3L

��ϰ��ϵ�д�
 �ƸԿ�����ҵ��ϵ�д�
�ƸԿ�����ҵ��ϵ�д� ��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
�����Ŀ