题目内容
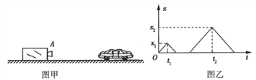
【题目】在光滑的水平桌面上有等大的质量分别为M=0.6kg,m=0.2kg的两个小球,中间夹着一个被压缩的具有Ep=10.8J弹性势能的轻弹簧(弹簧与两球不相连),原来处于静止状态.现突然释放弹簧,球m脱离弹簧后滑向与水平面相切、半径为R=0.425m的竖直放置的光滑半圆形轨道,如图所示.g取10m/s2 . 则下列说法正确的是( )

A. 球m从轨道底端A运动到顶端B的过程中所受合外力冲量大小为3.4Ns
B. M离开轻弹簧时获得的速度为9m/s
C. 若半圆轨道半径可调,则球m从B点飞出后落在水平桌面上的水平距离随轨道半径的增大而减小
D. 弹簧弹开过程,弹力对m的冲量大小为1.8Ns
【答案】AD
【解析】试题分析:释放弹簧过程中系统动量守恒、机械能守恒,以向右为正方向,
由动量守恒得:mv1﹣Mv2=0,由机械能守恒得:mv12+Mv22=EP,
代入数据解得:v1=9m/s,v2=3m/s;
m从A到B过程中,由机械能守恒定律得:
mv12=mv1′2+mg2R,解得:v1′=8m/s;
A、以向右为正方向,由动量定理得,球m从轨道底端A运动到顶端B的过程中所受合外力冲量大小为:
I=△p=mv1′﹣mv1=0.2×(﹣8)﹣0.2×9=﹣3.4Ns,则合力冲量大小为:3.4Ns,故A正确;
B、M离开轻弹簧时获得的速度为3m/s,故B错误;
C、设圆轨道半径为r时,飞出B后水平位移最大,由A到B机械能守恒定律得:mv12=mv1′2+mg2r,在最高点,由牛顿第二定律得:mg+N=m![]() ,m从B点飞出,需要满足:N≥0,飞出后,小球做平抛运动:2r=gt2,x=v1′t,当8.1﹣4r=4r时,即r=1.0125m时,x为最大,球m从B点飞出后落在水平桌面上的水平距离随轨道半径的增大先增大后减小,故C错误;
,m从B点飞出,需要满足:N≥0,飞出后,小球做平抛运动:2r=gt2,x=v1′t,当8.1﹣4r=4r时,即r=1.0125m时,x为最大,球m从B点飞出后落在水平桌面上的水平距离随轨道半径的增大先增大后减小,故C错误;
D、由动量定理得,弹簧弹开过程,弹力对m的冲量大小为:I=△p=mv1=0.9=1.8Ns,故D正确;
故选:AD.