题目内容
一质量为m=2kg的物体置于水平传送带上,随传送带一起以速度v1=2.0m/s向前运动,中途因受到一光滑挡板的阻碍而停止向前运动;现要用一平行于挡板的水平力F将物体以速度v2=1.5m/s沿着挡板拉离传送带,已知板与传送带运动方向垂直(如图所示),物体与传送带间的动摩擦因数为μ=0.3,试求拉力F和挡板对物体的弹力N的大小.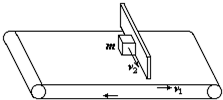

以传送带为参考系,物体有两个速度,一个是与传送带速度方向相反的2m/s,一个是拉离传送带的1.5m/s,所以合速度的方向与挡板夹角为:
tanα=
=
摩擦力的方向与这个速度方向相反.摩擦力大小为:f=μmg=6N.
则与拉离传送带方向相反的摩擦力大小为:f1=fsinα=6sinα=3.6N,F与这个分力大小相等方向相反
在传送带的速度方向上摩擦力大小为:f2=fcosα=6cos37=4.8N,N与这个分力大小相等速度相反.
答:拉力F为3.6N;档板对物体的弹力为4.8N.
tanα=
| 2 |
| 1.5 |
| 4 |
| 3 |
摩擦力的方向与这个速度方向相反.摩擦力大小为:f=μmg=6N.
则与拉离传送带方向相反的摩擦力大小为:f1=fsinα=6sinα=3.6N,F与这个分力大小相等方向相反
在传送带的速度方向上摩擦力大小为:f2=fcosα=6cos37=4.8N,N与这个分力大小相等速度相反.
答:拉力F为3.6N;档板对物体的弹力为4.8N.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
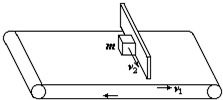 一质量为m=2kg的物体置于水平传送带上,随传送带一起以速度v1=2.0m/s向前运动,中途因受到一光滑挡板的阻碍而停止向前运动;现要用一平行于挡板的水平力F将物体以速度v2=1.5m/s沿着挡板拉离传送带,已知板与传送带运动方向垂直(如图所示),物体与传送带间的动摩擦因数为μ=0.3,试求拉力F和挡板对物体的弹力N的大小.
一质量为m=2kg的物体置于水平传送带上,随传送带一起以速度v1=2.0m/s向前运动,中途因受到一光滑挡板的阻碍而停止向前运动;现要用一平行于挡板的水平力F将物体以速度v2=1.5m/s沿着挡板拉离传送带,已知板与传送带运动方向垂直(如图所示),物体与传送带间的动摩擦因数为μ=0.3,试求拉力F和挡板对物体的弹力N的大小. 如图所示,水平的传送带以初速度v0=2m/s,加速度
如图所示,水平的传送带以初速度v0=2m/s,加速度
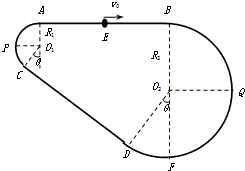 如图是放置在竖直平面内游戏滑轨的模拟装置,滑轨由四部分粗细均匀的金属杆组成:水平直轨AB,半径分别为R1=1.0m和R2=3.0m的弧形轨道,倾斜直轨CD长为L=6m,AB、CD与两圆形轨道相切,其中倾斜直轨CD部分表面粗糙,动摩擦因数为μ=
如图是放置在竖直平面内游戏滑轨的模拟装置,滑轨由四部分粗细均匀的金属杆组成:水平直轨AB,半径分别为R1=1.0m和R2=3.0m的弧形轨道,倾斜直轨CD长为L=6m,AB、CD与两圆形轨道相切,其中倾斜直轨CD部分表面粗糙,动摩擦因数为μ=