题目内容
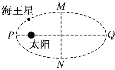
【题目】如图所示为两组平行板金属板,一组竖直放置,一组水平放置,今有一质量为m的电量为e的电子静止在竖直放置的平行金属板的A点,经电压U0加速后通过B点进入两板间距为d、电压为U的水平放置的平行金属板间,若电子从两块水平平行板的正中间射入,且最后电子刚好能从右侧的两块平行金属板穿出,A、B分别为两块竖直板的中点,求:
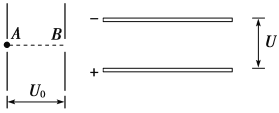
(1)电子通过B点时的速度大小;
(2)右侧平行金属板的长度;
(3)电子穿出右侧平行金属板时的动能和速度方向.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() ,
,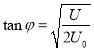
【解析】
(1)质子在加速电场中,电场力做正功eU0,由动能定理求解质子射出加速电场的速度.
(2)质子进入偏转电场后做类平抛运动,沿水平方向做匀速直线运动,位移大小等于板长L;竖直方向做匀加速直线运动,位移大小等于板间距离的一半,由牛顿第二定律求出加速度,由运动学公式求解板长L.
(3)在偏转电场中,电场力对质子做为![]() eU,根据动能定理,对全过程研究,求解质子穿出电场时的速度.
eU,根据动能定理,对全过程研究,求解质子穿出电场时的速度.
(1)在加速过程根据动能定理得:eU0=![]() mv02
mv02
解得到质子射出加速电场的速度![]()
(2)粒子在竖直方向:y=![]() d=
d=![]() at2,
at2,![]()
在水平方向:x=L=v0t
联立上式得到 ![]() d=
d=![]()
代入数据得
L=d![]()
(3)从刚开始到射出电场的过程中运用动能定理得:
![]() mv2=e(U0+
mv2=e(U0+![]() )
)
所以
![]()
速度方向与水平方向夹角φ满足
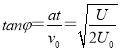

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目