题目内容
【题目】（18分）如图所示，MN是水平轨道，NP是倾角θ=45°的无限长斜轨道，长为L=0.8m的细线一端固定在O点，另一端系着质量为mB=2kg小球B，当细线伸直时B球刚好与MN轨道接触但没有挤压。开始时细线伸直，B球静止在MN轨道上，在MN轨道上另一个质量为mA=3kg小球A以速度v0向右运动。（不计一切摩擦及空气阻力，重力加速度g=10m/s2）
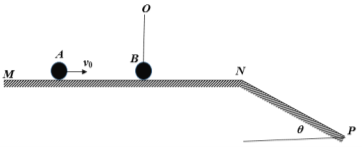
（1）若A、B球发生弹性碰撞后B能在竖直面内做圆周运动，求v0的取值范围。
（2）在满足（1）的条件下，轨道NP上有多长的距离不会被A球击中？
【答案】（1）
m/s或
m/s （2）
m
【解析】（1）A、B两球发生弹性碰撞，由动量守恒定律得
（2分）
由机械能守恒定律得
（2分）
解得
，
（1分）
碰后B球在竖直面内做圆周运动，有两种情况：
第一种情况，B球在竖直面内做完整的圆周运动，则它到最高点的速度
（1分）
由机械能守恒定律得：
（1分）
解得：m/s（1分）
第二种情况，B球运动的最大高度不超过L（1分）
由机械能守恒定律得：
（1分）
解得：
（1分）
v0的取值范围为m/s或m/s（1分）
（2）由上可知：碰后A球的速度
m/s或
m/s（1分）
A球离开水平轨道后做平抛运动，有
，
，又由几何关系知
（2分）
解得A球落到斜轨道上与N点的距离
（1分）
解得：
m或
m（1分）
故轨道NP上不会被A球击中的距离
（1分）
练习册系列答案
应用题作业本系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
